
Perspectives on Enquiry & Evidence
Cytel's blog featuring the latest industry insights.

April 17, 2024
Written by Grace Hsu, Evie Merinopoulou, and Jason Simeone To establish treatment efficacy and safety, regulatory and...
Read article

April 15, 2024
Data-Centric Approaches to Streamline the Clinical Workload
In the context of clinical trials, reducing the workload of the clinical team without compromising data quality is...
Read article

April 12, 2024
The New EU HTA Landscape: Insights on Indirect Evidence
How should health technology developers prepare for future market access activities in Europe? Numerous discussions...
Read article

April 10, 2024
Orphan Drug Designation for Rare Diseases
Orphan drug designation is a regulatory status granted to pharmaceuticals developed for the treatment of rare diseases....
Read article

April 8, 2024
Career Perspectives: A Conversation with Joshua Murray
In this latest edition of the Career Perspectives series, we are excited to introduce our readers to Joshua Murray,...
Read article

April 5, 2024
Commercial and Open-Source Software Synergy for Clinical Trial Design
Written by Sydney Ringold, Customer Success Manager, and Kevin Trimm, Chief Product Officer In an ever-changing...
Read article
April 3, 2024
Developing a New Drug Candidate: From Nonclinical to First-in-Human
Thank you to Charlotta Gauffin, Chief Scientific Officer at Dicot, for joining us for our recent webinar, “The Road to...
Read article

April 2, 2024
The FDA’s New Draft Guidance on DMCs: What to Know
Data monitoring committees (DMCs) review ongoing clinical trial data to make recommendations regarding trial conduct...
Read article

March 20, 2024
Key Elements and Implications of the Draft EU JCA Implementing Act
Written by Lydia Vinals, PhD, and Grammati Sarri, PhD The draft Implementing Act of the EU Health Technology Assessment...
Read article

March 13, 2024
Understanding Group Sequential Designs
Group sequential clinical trial designs — a type of adaptive clinical trial design — have emerged as a powerful tool in...
Read article

March 11, 2024
Quantitative Strategies for Rare Disease Clinical Trials
In 2023, rare diseases accounted for 30% of product pipeline under development, about half of which comprising...
Read article

March 4, 2024
Career Perspectives: A Conversation with Arnold van Aswegen
In this new installment of the Career Perspectives series, we had the privilege of interviewing Arnold van Aswegen,...
Read article
February 26, 2024
Sample Size Re-Estimation for Rare Disease Clinical Trials
Written by Boaz N. Adler, MPA, Director, Global Product Engagement, and Valeria Mazzanti, MPH, Associate Director,...
Read article

February 23, 2024
Metadata Repositories: Overcoming Challenges with Automation
Written by Angelo Tinazzi, Nicolas Rouillé, and Sebastià Barceló In the realm of standards management, companies of all...
Read article

February 20, 2024
Negative Binomial Distribution in Group Sequential Designs
In clinical trials based on count data, the aim is to compare independent treatment groups in terms of the rate of...
Read article

February 14, 2024
Erika Spens on Developing Your Regulatory Strategy
During drug development, a comprehensive regulatory strategy is key for saving time and money. There are many common...
Read article

February 13, 2024
Strategies to Overcome Limited Patient Population Challenges in Rare Disease Studies
Written by Boaz N. Adler, MPA, Director, Global Product Engagement, and Valeria Mazzanti, MPH, Associate Director,...
Read article

February 2, 2024
The Living Model Approach for Systematic Literature Reviews
When building a disease model or an economic model, the assumption has been that updates to such models should only...
Read article

January 26, 2024
Parameter Optimization of Multi-Arm Multi-Stage Designs
Innovations in the process of designing adaptive clinical trials have unlocked new possibilities for designing and...
Read article

January 22, 2024
How to Save Time and Limit Costs toward First-in-Human Clinical Trials
Regulatory guidelines outline all crucial studies and documentation that should be in place before a drug product can...
Read article

January 19, 2024
Accelerated DMC Safety Reports for Biotech’s Central Nervous System Studies: A Case Study
Independent data monitoring committees help to ensure patient safety and uphold trial integrity. In Central Nervous...
Read article

January 17, 2024
Late-Stage Clinical Development Strategy: Trade-Offs and Decision-Making in the Confirmatory Setting
Despite accumulating learnings from early phases, several uncertainties remain to be addressed when designing pivotal...
Read article

January 15, 2024
Navigating the Clinical Development Landscape: Insights for Success in 2024
After explosive and frenetic activity in the clinical trial industry during the COVID era, the past two years have seen...
Read article

January 10, 2024
Optimizing Early Clinical Development Strategy
A clinical development strategy is a comprehensive plan designed to establish the safety and efficacy of new...
Read article

January 3, 2024
New FDA Data Submission Requirements and Substantial Changes
Ten years ago this month, in January 2014, the FDA issued the first version of its Technical Conformance Guide (by...
Read article

December 29, 2023
The Top Most-Read Posts of 2023
What a year! Perspectives has explored a myriad of topics this year within clinical development — from adaptive trial...
Read article

December 27, 2023
Top Data Submission and Data Integration Posts of 2023
Perspectives covers a wide range of topics related to data submission and data integration, from ISS and ISE best...
Read article

December 22, 2023
Top Therapeutics Development Topics of 2023
Perspectives covers a wide range of topics within therapeutics development from advice on regulatory submission to...
Read article

December 20, 2023
Top Real-World Evidence and Real-World Data Topics of 2023
Perspectives covers a wide range of topics related to real-world evidence and real-world data, from overcoming health...
Read article

December 15, 2023
The Value of an Optimized Clinical Data Strategy: How Small Changes Can Make a Big Difference
In clinical trials, high-quality data is essential. It drives the drug development decision-making process and is a...
Read article

December 8, 2023
Discussions with the FDA and Ensuring Data Submission Success
Regular technical discussions with the FDA play a critical role in ensuring data submission success. These discussions...
Read article

December 6, 2023
Drug Manufacturer Auditing: Ensuring Quality, Control, and Safety
Chemistry, Manufacturing, and Controls (CMC) is a critical component of drug product development. As a Senior...
Read article

December 4, 2023
Preserving Trial Integrity After Receiving an Unanticipated IDMC Recommendation
Independent data monitoring committees review unblinded clinical trial data and issue recommendations to designated...
Read article

December 1, 2023
Leveraging Real-World Data for Comparison Using Synthetic Control Arms
Last week, Robert Szulkin, Research Principal, Real World Evidence, discussed the need for real-world evidence studies,...
Read article

November 29, 2023
Don’t Forget the Development of Your Placebo: Overcoming Common Obstacles
A clinical trial is usually performed using some kind of comparator. This could be another drug on the market, or a...
Read article

November 24, 2023
Epidemiological Methods to Tackle Real-World Evidence Challenges
Regulatory requirements regarding documentation for new medicines are constantly evolving. Previously, randomized...
Read article

November 20, 2023
Guidelines Are Not Instruction Manuals: Customize Your Way to First-in-Human Clinical Trials
Interpreting all guidelines before your first-in-human clinical trials can be overwhelming. While guidelines are...
Read article

November 17, 2023
FSP Behind the Scenes with Nandan Kothavale, Programming Senior Team Lead
Cytel’s Functional Service Provision (FSP) teams work on exciting projects with biotech and pharmaceutical companies as...
Read article

November 13, 2023
First-in-Human Drug Substance and Formulation: The Challenge of Achieving Flexibility and Quality
For nonclinical studies that precede Phase I, a drug formulation in high doses and concentrations is required. While...
Read article

November 10, 2023
Conduct of IDMCs for Cell and Gene Therapy Trials
Independent data monitoring committees review unblinded clinical trial data and issue recommendations to designated...
Read article

November 8, 2023
Aligning Clinical Trial Design with Investment Priorities
Written by Natalia Muehlemann, Vice President, Clinical Development, and Ari Brettman, Senior Managing Director,...
Read article

November 6, 2023
Ulrika Andersson on First-in-Human Clinical Trial Development
The first-in-human trial, which aims to show the safety and tolerability of a new drug, is a major milestone for any...
Read article

November 3, 2023
Reinforcement Learning: A Promising Tool for Predicting Optimal Treatment in Complex Diseases
Written by Fei Tang and Evie Merinopoulou Reinforcement Learning (RL), a crucial component of machine learning (ML),...
Read article

November 1, 2023
The Changing Landscape of the Pharmaceutical Industry: A Preview of Cytel’s Contributions at PHUSE EU 2023
It feels like just yesterday I attended my first PHUSE conference back in 2005 in Heidelberg, Germany. Fast forward 19...
Read article

October 30, 2023
Managing Uncertainty: Simulation-Based Assurance in Clinical Trial Design
The past two decades have seen the adoption of great innovation in clinical trial design. Statisticians have risen to...
Read article

October 27, 2023
News from ESMO: Challenging the Status Quo of Early Phase Clinical Trial Design — Moving from “Why” to “How”
Written by Natalia Muehlemann, Vice President, Clinical Development; Martin Frenzel, Research Principal, Statistical...
Read article

October 25, 2023
Unravelling PICO: The Pillars of the European Joint Clinical Assessment
The European Union (EU) health technology assessment (HTA) regulation aims to improve the availability of innovative...
Read article

October 23, 2023
Experiencing the CBER: Anticipating Unique Challenges
The Center for Drug Evaluation and Research (CDER) and the Center for Biologics Evaluation and Research (CBER) are the...
Read article

October 20, 2023
Mind the Health Gap: Is It Time to Reliably Measure the Impact of Health Inequity in Product Development and Assessment? Yes, It Is.
Written by Grammati Sarri and Yannis Jemiai The spotlight for this year’s World Evidence-Based Healthcare Day (EBHC)...
Read article

October 18, 2023
Preparing Your Integrated Summaries of Safety and Effectiveness: Best Practices
Written by Angelo Tinazzi and Florence Le Maulf Integrated Summaries of Safety (ISS) and Integrated Summaries of...
Read article

October 13, 2023
Looking to the Future — Improving Diagnosis and Prognosis of Eye Conditions with Artificial Intelligence
Written by Alind Gupta, Cytel; Haridarshan Patel, Horizon Therapeutics; and Jason Simeone, Cytel Ophthalmology is...
Read article

October 11, 2023
Global Planning to Local Execution Market Success
Moving beyond static evidence development to ensure local market access success; responding to recent changes in...
Read article

October 10, 2023
FSP Behind the Scenes with Brooke Smith, Senior Biostatistician
Cytel’s Functional Service Provision (FSP) teams work on exciting projects with biotech and pharmaceutical companies as...
Read article

October 6, 2023
Writing a Successful Study Protocol for Real-World Evidence Studies
Real-world evidence studies are becoming increasingly popular in pharmaceutical development. But to ensure such studies...
Read article

October 4, 2023
How to Ensure Your Adaptive Trial Is Appropriate for Regulatory Submission
Adaptive clinical trial designs have become increasingly popular among developers and investors due to the many...
Read article

October 2, 2023
A Better Way to Track Medication Adherence
Patients’ adherence to the medications or treatment regimens prescribed to them by their clinicians is an important...
Read article

September 29, 2023
Innovative Clinical Trial Design: Commercial vs Open-Source Software? Why Not Both?
In the ever-changing field of clinical trial design, there is often a need to evaluate design options quickly and...
Read article

September 25, 2023
Reducing Independent Data Monitoring Committee Timelines: A Focus on Formal Interim Analyses
As the pressure to reduce timelines rises across the industry, independent data monitoring committees (IDMCs) — which...
Read article

September 22, 2023
Myth Busting: Master Protocol Edition
Interest and appetite for master protocols is growing as sponsors consider opportunities in various therapeutic areas...
Read article

September 20, 2023
FSP Behind the Scenes with Anwaya Joshi, Programming Senior Team Lead
Cytel’s Functional Service Provision (FSP) teams work on exciting projects with biotech and pharmaceutical companies as...
Read article

September 18, 2023
Cytel Publishes Inaugural Sustainability Report
With the ongoing changes inherent in the life sciences industry comes heightened expectations for companies to take...
Read article

September 13, 2023
Setting Expectations for Formal Interim Analyses with Independent Data Monitoring Committees
Independent data monitoring committees (IDMCs) review ongoing clinical trial data to make recommendations regarding...
Read article

September 11, 2023
How to Ask the Right Questions at an Authority Meeting
As a drug developer, you have to live with the answers and comments you get from regulatory authorities. Therefore,...
Read article

September 8, 2023
Synthetic Control Arms: Leveraging Real-World Data for Comparison in Single-Arm Trials
Single-arm trials, unlike placebo-controlled randomized control trials, forgo the use of a placebo or standard-of-care...
Read article

September 1, 2023
Key Considerations in Planning Your Clinical Data Strategy
Data is the cornerstone of any clinical trial, driving the decision-making process of drug development, and is a...
Read article

August 30, 2023
FSP Behind the Scenes with Jeff Thompson, R Senior Statistical Programmer
Cytel’s Functional Service Provision (FSP) teams work on exciting projects with biotech and pharmaceutical companies as...
Read article

August 28, 2023
How to Create and Optimize a Clinical Development Plan
A clinical development plan — a comprehensive strategy for developing an investigational product through regulatory...
Read article

August 25, 2023
Preparing and Concluding Your FDA Data Submission, and More Insights on Data Submission and Data Integration
For several years, CDISC and Regulatory Data Submission expert Angelo Tinazzi has authored the series, The Good Data...
Read article

August 22, 2023
Adaptive Multi-Arm Multi-Stage Designs: A Comparison of Methods
Written by Cyrus Mehta and Heather Struntz The significant time and cost, as well as high failure rates, of clinical...
Read article

August 18, 2023
The Advantages of Forecasting Enrollment with a Model-Based Approach
The most common cause for incomplete Phase III trials is enrollment. Indeed, as many as 37% of trials miss...
Read article

August 14, 2023
The Evolution of Open-Source Initiatives and New Standards Development for the Data Submission of the Future
In the first part of this post, I discussed the ongoing revolution, or maybe I should say evolution, we are living...
Read article

August 11, 2023
Demonstrating Value in Real Time with Living Models for Systematic Literature Reviews
Systematic literature reviews are essential for proving product value to health authorities, clinicians, and payers,...
Read article

August 9, 2023
Standards and Open Source Hand-in-Hand: Leveraging Automation to Expedite Drug Market Request Review Process
How do you envision the future of data submission? Last week, I had the privilege of presenting the topic “Standards...
Read article

August 4, 2023
Bayesian Methods for Strategic Clinical Trial Design
“There is always the risk that interim analyses might occur after the Sufficient Information Threshold has been...
Read article

August 1, 2023
Dynamic Bayesian Borrowing to Bolster Limited Sample Sizes in Rare Indications
Evaluating the efficacy and safety of novel therapies in rare indications can be challenging due to the difficulty of...
Read article

July 28, 2023
Embracing AI and ML in Medical Devices: FDA’s Total Product Lifecycle-Based Regulatory Framework
Written by Fei Tang, RWE Senior Research Consultant, and Paul Arora, Assistant Professor (Status), Dalla Lana School of...
Read article

July 14, 2023
Real-Life Data-Sharing and EU Joint Clinical Assessments: Is Closing this Chasm a Mission Impossible?
Written by Grammati Sarri, David Smalbrugge, Andreas Freitag, and Evie Merinopoulou The vision of a single, centralized...
Read article


June 20, 2023
New FDA Guidelines on Pediatric Studies and Potential Effects on Opportunities for Market Exclusivity
Legislation on pediatric studies has existed for more than 20 years in the US, yet additional guidance from the FDA has...
Read article

June 14, 2023
Embracing Innovation: Exploring the Design of Umbrella and Basket Trials
Medical research has come a long way in recent years, fueled by innovative trial designs that challenge traditional...
Read article

June 9, 2023
Maximizing Study Momentum: A Case Study in Accelerated DMC Safety Report Creation through IDMC Solutions
In the ever-evolving landscape of clinical development, the need for robust evaluation of interim clinical data through...
Read article

June 7, 2023
A Spotlight on FSP Programming
Since its founding in 1987, Cytel has been home to some of the most passionate, creative, and talented experts in the...
Read article

June 5, 2023
Maria Lundberg on a Holistic Approach to Therapeutics Development
Cytel recently announced the launch of its Therapeutics Development Team, bringing together quantitative,...
Read article

June 2, 2023
Presenting Clinical Data for Regulatory Submission: A Stats Perspective
Data submissions are very regulated, but every drug and drug development are different. Therefore, the data presented...
Read article

May 24, 2023
It’s Time to Move, Time to Move to Define-XML 2.1
As of March 2023, specifically for any study started on or after March 15, 2023,1 for the submission of SEND, SDTM, and...
Read article

May 22, 2023
New CADTH Guidance on RWE Is Now Available, but Critical Aspects Are Still Missing
By Grammati Sarri, Evie Merinopoulou, Vinusha Kalatharan, and Jason Simeone The Canadian Agency for Drugs and...
Read article


May 10, 2023
FDA Increases Calls for Manufacturers to Ensure Trial Diversity, but Does It Fall Short of Addressing Health Inequalities in Product Development?
The evidence is staggering on the unequal health burdens experienced by specific patient groups defined by ethnic,...
Read article

May 5, 2023
Scott Gaines on the Power of Simulation-Guided Design to Handle Increasingly Complex Clinical Trials
As clinical trials become more complex, simulation-guided design approaches are crucial. For this edition of the...
Read article

May 3, 2023
Reflections on the RCT DUPLICATE Study and Increasing Confidence in Real-World Evidence
With input by Alind Gupta, Louis Dron, and Jason Simeone. Randomized clinical trials (RCTs) have long been considered...
Read article

April 26, 2023
New Ebook: “The Good Data Doctor on Data Submission and Data Integration”
Regular technical discussions with the FDA play a critical role in ensuring data submission success. These discussions...
Read article

April 25, 2023
How Target Trial Emulation Can Take the Guesswork Out of Comparative Effect Estimates in Medicare Drug Price Negotiation
An interview with Miguel Hernán, Harvard University Kolokotrones Professor of Biostatistics and Epidemiology On March...
Read article

April 24, 2023
APAC Biopharma Industry Insights: Trends, Opportunities, and Challenges
In the last 10 years, the Asia-Pacific (APAC) region has become a hotspot for clinical trials: the region contributed...
Read article

April 21, 2023
CDISC Europe 2023: A Preview
It was early March 2020, after the world was hit by the Covid-19 pandemic, that those of us on the CDISC Eu committee...
Read article

April 18, 2023
Navigating Comparative Effectiveness in the Inflation Reduction Act: Methodological Approaches for Healthcare Challenges
The Inflation Reduction Act (IRA), passed in August 2022, marks a significant shift in the US healthcare landscape,...
Read article

April 14, 2023
Data Challenges (and Solutions) for Externally Controlled Trials
Real-world data and evidence are increasingly being used in health care decisions and publications. However, there are...
Read article

April 11, 2023
Overcoming the Shared Effect Modifier Assumption with Network Meta-Interpolation
Commonly used methods to handle the complexities of effect modification in indirect treatment comparisons (ITCs) often...
Read article

April 5, 2023
Comparative Effectiveness: Methods and Techniques for Better Decision-Making
Health technology assessment (HTA) submissions require cost effectiveness analyses based on comparative effectiveness...
Read article

March 24, 2023
Winter Weekend Read Roundup
Last week, we featured our final Winter Weekend Read, the last in a series designed to showcase our complimentary...
Read article

March 21, 2023
Retrospective Claims Data Analysis Unlocks Discovery in Multiple Sclerosis Research
One of the lesser-known complications associated with Multiple Sclerosis is a higher risk of serious infections (SIs)....
Read article

March 17, 2023
Optimizing Small Clinical Trials with Simulation-Guided Design: A Case Study
Smaller clinical trials can be optimized in significant ways using simulation-guided design. A small biotech studying...
Read article

March 13, 2023
Industry Voices: Yannis Jemiai on Simulation-Guided Design and the Changing Landscape of Clinical Trial Strategy
Many industries have long since adopted the practice of modeling and simulating experimental scenarios. And despite...
Read article

March 8, 2023
New Linked Database Expands Potential of RWE: A Unique Opportunity for Multiple Sclerosis Research
Real-world data has been increasingly used to answer questions related to the course, prognosis, and treatment of...
Read article

March 7, 2023
Can RWE Help Restore Decades of Health Inequalities? Yes, and Here’s How
Health inequalities are an enduring issue that can be exacerbated by clinical trial recruitment that does not reflect...
Read article

March 3, 2023
Multiple Myeloma Research Benefits from Living Model SLR: A Case Study
The speed of scientific discovery has been outpacing the ability of researchers to accumulate and integrate constantly...
Read article

February 24, 2023
Demystifying Synthetic Control Arms
Last week, Cytel Director & Research Principal Louis Dron discussed new FDA guidance on the design and conduct of...
Read article

February 22, 2023
Simulation-Guided Design for Biotechs
Simulation-guided design is quickly becoming a novel feature of modern drug development. Its foundational promise is to...
Read article

February 14, 2023
FDA Guidance on the Design and Conduct of Externally Controlled Trials — What to Watch
The U.S. FDA has recently provided specific guidance[i] on the design and conduct of trials incorporating an external...
Read article

February 9, 2023
Supercharging Quantitative Decision-Making with Simulation-Guided Trial Design
Those familiar with simulation-guided design (SGD) know that it can be used for a wealth of clinical trial options:...
Read article

February 8, 2023
The Facts in the Case of Subject X
Over the past years, probably the entire last decade, there have been several discussions on how to handle multiple...
Read article

February 3, 2023
Focal Points and Monetization: New Uses of Pareto Frontiers in Clinical Development
For clinical development and research and development teams, the Pareto Frontier can perform two functions. Let’s take...
Read article

January 31, 2023
Linked Data Studies: Improving the Way We Do Observational Research in Germany
Asthma affects more than 235 million people worldwide, and due to lacking effective implementation of clinical...
Read article

January 27, 2023
To Adapt or Not to Adapt? A Decision Framework
Should your clinical trial be adaptive? Trials that include a prospectively planned modification based on an interim...
Read article

January 25, 2023
Bayesian Approach in Oncology Trials
People think in Bayesian terms all the time: we use prior information and the evidence at hand to make decisions in our...
Read article

January 23, 2023
Design Considerations for Early Phase Trials of Immuno-oncology Drugs
Ever since the first immune checkpoint inhibitor was approved for market nearly twelve years ago, the industry has...
Read article

January 20, 2023
Strategic Clinical Trial Design Unlocks Innovative Funding Opportunity
A small biotech’s conventional carcinoma trial design was too expensive to implement and did not offer the opportunity...
Read article

January 17, 2023
Bayesian Strategies in Rare Diseases
When it comes to rare diseases, a handful of major challenges to drug development arise. Bayesians strategies have...
Read article

January 13, 2023
Bayesian Methods across the Clinical Development Journey
Bayesian methods, with their ability to facilitate flexibility and learning, are often associated with early-phase...
Read article

January 12, 2023
Why Are There Not More Bayesian Clinical Trials?
Statistical methods have long been fundamental to drug development, and advancements in the last few decades in...
Read article

January 6, 2023
Simulation-Guided Design Is Reshaping Clinical Trial Strategy
You may have heard that our clinical trial strategy platform Solara® won the Fierce Life Sciences award for Technology...
Read article

January 4, 2023
A Look Ahead for 2023
Returning to Cytel after the winter holidays, I am excited to begin a year that will likely prove memorable for both my...
Read article

December 29, 2022
Top Perspectives Articles of 2022
Perspectives on Enquiry and Evidence explores a wide variety of topics within clinical trial design and data science in...
Read article

December 27, 2022
Top Bayesian Topics of 2022
Bayesian methods have been playing a key role in transforming clinical research, providing a variety of new...
Read article

December 21, 2022
Top Interviews of 2022: Industry Voices and Career Perspectives
Perspectives on Enquiry and Evidence features two recurring interview series: Our new Industry Voices series, in which...
Read article

December 19, 2022
Top Adaptive Clinical Trial Topics of 2022
Adaptive trial designs – that is, trials that include a prospectively planned modification based on an interim analysis...
Read article

December 16, 2022
Topics in Bayesian Statistical Methods
Bayesian methods have been playing a key role in transforming clinical research, and Bayesian topics are frequently...
Read article

December 14, 2022
Accrual When Starting a Platform Trial vs. in a Stand-Alone Trial
When evaluating the efficacy of a candidate investigational therapy, a standard clinical trial paradigm is to conduct a...
Read article

December 9, 2022
(Re)Integration Dilemma: Integrated Summaries of Safety and Effectiveness
As promised in my last post prior to PHUSE-EU Connect, I’d like to now share some reflections on my “Integration...
Read article

December 6, 2022
Career Perspectives: A Conversation with Veronica Chan
In this edition of the Career Perspectives series, I spoke with Veronica Chan, Principal Clinical Data Manager at...
Read article

December 2, 2022
Celebrating 35 Years of Innovation and Impact: An Interview Series
For 35 years, Cytel’s scientific rigor and operational excellence have enabled biotech and pharmaceutical companies to...
Read article

November 29, 2022
Bayesian Adaptive Clinical Trial Designs: INLA vs. MCMC
Bayesian methods have continuously played a key role in transforming clinical research in therapeutic areas such as...
Read article

November 18, 2022
Industry Voices: Dr. Parvin Fardipour on New Horizons in Data Science
In the following interview, Dr. Parvin Fardipour, Quantitative Strategies & Data Science, sits down with Heather...
Read article

November 14, 2022
Network Meta-Interpolation: Effect Modification Adjustment in Network Meta-Analysis Using Subgroup Analyses
When conducting network meta-analysis (NMA) – that is, a technique that involves comparing multiple treatments...
Read article

November 9, 2022
Career Perspectives: A Conversation with Malte Stein
In this edition of the Career Perspectives series, I interview Malte Stein, Senior Biostatistician. Malte owned the...
Read article

November 8, 2022
A Preview of Cytel’s Contributions to PHUSE EU 2022
Although many of you can’t wait for the start of the Football World Cup 2022 (less than two weeks while I’m writing),...
Read article

November 3, 2022
Cytel at ISPOR Europe: Two Workshops
Cytel will be represented at over 60 presentations at ISPOR Europe 2022, with more issue panels and workshops than any...
Read article

November 2, 2022
Bayesian Hierarchical Modelling for Histology-Independent Therapies
Pharmaceutical research in oncology is increasingly focused on the development of therapies targeted at newly...
Read article

October 28, 2022
Measuring Robustness of Clinical Trial Designs with Pressure Tests
Integrating the “pressure testing” of clinical trial designs into the process of creating a strong clinical trial...
Read article


October 24, 2022
Cyrus Mehta on the Founding of Cytel
On the occasion of Cytel’s 35th anniversary, co-founder Professor Cyrus Mehta sits down with Dr. Esha Senchaudhuri to...
Read article



October 18, 2022
Nitin Patel on 35 Years of Technological Innovation
On the occasion of Cytel’s 35th anniversary, co-founder Professor Nitin Patel sits down with Dr. Esha Senchaudhuri to...
Read article

October 14, 2022
Career Perspectives: A Conversation with Nicolas Rouillé
In this edition of the Career Perspectives series, I interview Nicolas Rouillé, Senior Director, Statistical...
Read article

October 13, 2022
Cytel at ISPOR Europe: Top Presenter of Issue Panels and Workshops
ISPOR Europe, the leading global conference for health economics and outcomes research (HEOR) and real-world evidence...
Read article

October 11, 2022
Joshua Schultz on the Evolution of Cytel
On the occasion of Cytel’s 35th anniversary, our CEO Joshua Schultz sits down with Dr. Esha Senchaudhuri to discuss the...
Read article

October 5, 2022
Platform Trials, Can they Benefit Animal Studies?
Master protocols and platform clinical trials have become an innovative and efficient approach to testing multiple...
Read article

October 4, 2022
MCMC vs. INLA in Bayesian Adaptive Clinical Trial Designs
Integrated Nested Laplacian Approximations (or INLA) are now starting to be used by statisticians as a key tool for...
Read article

October 3, 2022
Bayesian Methods for Historical Borrowing: Conjugate Priors
The wider availability of electronic health data, medical registries, and even larger proprietary datasets means that...
Read article


September 28, 2022
Statistical Leaders and the Future of Drug Development
The landscape of drug development has changed dramatically over the last few decades, and effective statistical leaders...
Read article

September 27, 2022
Data Capture and Data Sharing During the COVID-19 Pandemic
On Louis Dron et al., “Data Capture and Sharing in the COVID-19 Pandemic: A Cause for Concern,” The Lancet 4 (10) (2022)
Read article

September 23, 2022
Adaptive Trials at the Mainstream of Drug Development
Adaptive trial designs – that is, trials that include a prospectively planned modification based on an interim analysis...
Read article

September 16, 2022
Raising Awareness for Additional FDA Data Standards Submission Recommendations (Part II)
In the first part of this article, I raised awareness of the availability of additional FDA guidances containing CDISC...
Read article

September 15, 2022
U.S. Drug Pricing Reform: Potential Impact on Pharma HEOR Evidence Generation
On August 16, 2022, President Biden signed into law the Inflation Reduction Act of 2022, which includes U.S. drug...
Read article

September 12, 2022
On Frequentist and Bayesian Sequential Clinical Trial Designs
In clinical trials, patient enrollment is often staggered, with data collected sequentially. When designing a clinical...
Read article

September 9, 2022
Developing Synthetic Control Arms Using Bayesian Models
A new trend has emerged over the last decade that has changed the way many clinical trials are conducted. Unlike...
Read article

September 8, 2022
Cytel Present at the ASA Biopharmaceutical Section Regulatory Workshop
The American Statistical Association Biopharmaceutical Section, in cooperation with the FDA Statistical Association,...
Read article

September 2, 2022
Summer Weekend Read Roundup
Last week, we featured our final Summer Weekend Read, the last in a series designed to showcase some of our most recent...
Read article

August 30, 2022
Understanding the Economic Benefits of Platform Trials
Many thanks to Kyle Wathen and Behnam Sharif for their input on this post.
Read article

August 26, 2022
Discover the Value of an Optimized Clinical Data Strategy
To continue our Summer Weekend Reads series, Cytel presents “Discover the Value of an Optimized Clinical Data Strategy”...
Read article

August 25, 2022
Cytel Presents at ICPE 2022
The International Society for Pharmacoepidemiology is hosting its “ICPE 2022: Advancing Pharmacoepidemiology and...
Read article


August 18, 2022
Highlights from JSM 2022
The American Statistical Association’s annual Joint Statistical Meeting (JSM) gathered over 6,500 attendees from 52...
Read article




August 4, 2022
Career Perspectives: Interview with Allison Luccock
In this edition of the Career Perspectives series, I interview Allison Luccock, Director of Business Operations for...
Read article

August 3, 2022
The Uses of Bayesian Methods in Late-Phase Clinical Trial Strategy
A number of late-phase clinical trial sponsors remain hesitant to employ Bayesian approaches in confirmatory settings,...
Read article


July 28, 2022
New Directions in Indirect Treatment Comparisons
When new treatments are compared with existing therapies in clinical care, population-adjustment techniques need to...
Read article

July 27, 2022
Adaptive Designs Are Re-Defining Drug Development – Learn What's New
Written by Jing Ping Yeo and Charles Warne Adaptive designs are studies that “include a prospectively planned...
Read article

July 26, 2022
7 Ways RWD Is Transforming Clinical Research
To watch this webinar and others from this introductory series, click the link below. The ability to draw on electronic...
Read article


July 20, 2022
The Case for Network Meta-Interpolation to Handle Effect Modifiers in Indirect Treatment Comparisons
When performing indirect treatment comparisons, effect modification can create complexities in the event of high...
Read article


July 13, 2022
5 Steps to Adjust for Effect Modifiers for Treatment Comparisons
Many thanks to Grammati Sarri and Michael Groff for their comments in developing this blog. An indirect treatment...
Read article

July 12, 2022
Strategies for Selecting New Indications for a Platform Trial
Thanks to Dr. Kyle Wathen for comments on this blog. The increasing use of platform trials for the testing of a wide...
Read article

July 7, 2022
Using Quantitative Bias Analysis in Real World Data Strategy
The gold standard for assessing the efficacy for a medicine continues to be RCTs, however, for many reasons (disease...
Read article

June 29, 2022
Platform Trials, Master Protocols, and Challenges in Execution
How can we build an efficient statistical protocol for a clinical trial, if we do not know the therapies that will be...
Read article

June 28, 2022
Career Perspectives: Reflecting at 10 Years in Cytel FSP
Founded in 1987 by Cyrus Mehta and Nitin Patel, research scientists at Harvard University and MIT respectively and...
Read article

June 22, 2022
How to Determine if Your Clinical Trial Has Sufficient Data?
It can be difficult to estimate just how much time and data you need to address the multitude of considerations that...
Read article

June 15, 2022
Raising Awareness for FDA Data Submission Recommendations (I)
For years CDISC data standards implementers have struggled to find good implementation examples and use cases beside...
Read article

June 14, 2022
6 Key Trials for Understanding Adaptive Designs for Clinical Trials
Suppose you had to choose six clinical trials intended for registration with regulatory agencies, only six, to explain...
Read article

June 13, 2022
Driving Global Data Collaboration for COVID-19
The International COVID-19 Data Alliance (ICODA) was formed to address the challenge of generating rapid and rigorous...
Read article
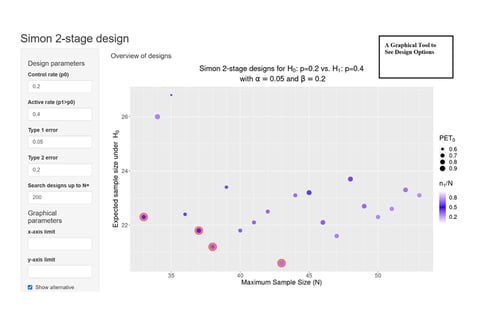
June 8, 2022
On Kappler's 'Graphical Comparison of Simon two-stage designs'
Clinical researchers, seeking to understand the statistical benefits of a common Phase 2 oncology design, now have a...
Read article

June 7, 2022
Continuous Monitoring for Blinded Sample Size Reestimation
In most instances of blinded sample size re-estimation, the timing of the interim analysis that determines whether the...
Read article

June 6, 2022
The TOGETHER Trial Journey: Interview with Ofir Harari
The award-winning TOGETHER Trial was designed with the vision of ensuring that COVID-19 therapies are both effective...
Read article

June 2, 2022
Digital Transformation for Clinical Trials
How can clinicians at the forefront of modern clinical trials and statisticians at the forefront of advanced...
Read article

May 31, 2022
What it means to be a lead analyst on a Global COVID-19 Trial
The TOGETHER Trial for COVID-19 therapies, designed by clinical trial specialists at Cytel won the Society for Clinical...
Read article

May 27, 2022
How to Use a Living HTA Approach to Demonstrate Value in Real-Time
When submitting systematic literature reviews to a Health Technology Assessment authority, high volumes of research...
Read article

May 26, 2022
Method of Estimation with application to the COVID-19 Pandemic
When constructing estimands a key question that arises is how to handle intercurrent events and missing data. In a...
Read article

May 24, 2022
Leveraging Advanced Statistical Software to Optimize Clinical Development
Traditionally, clinical trials are expensive, long in duration, and have low success rate. But with the advent of rich...
Read article
May 17, 2022
Society of Clinical Trials names TOGETHER "Trial of the Year"
Early in the pandemic, it became clear that many of the COVID-19 therapies being tested in wealthier nations, were not...
Read article

May 16, 2022
Cytel & ARCS Collaborate to Strengthen Early Phase Capabilities
A combination of industry and policy forces have recently changed the shape of Australia’s R&D sector, making it a...
Read article

May 12, 2022
Estimator Choice in Synthetic Control Arm Analyses
Synthetic control arm (SCA) methods are statistical methods that are seeing rapidly increasing use in comparative...
Read article

May 5, 2022
Interview with Grammati Sarri on Moderating an Issue Panel 2022
While randomized control trials remain the industry gold-standard for regulatory and reimbursement submissions, there...
Read article

May 4, 2022
Optimizing Human-Machine Partnership for Up-To-Date Evidence
If you are a pharmaceutical or biotech company seeking to enter the market with a new drug, you need to submit a...
Read article

May 3, 2022
Adaptive Designs for Early Phase Development: Are the questions right?
In 2005, Pfizer launched a Phase 1 trial for the kinase inhibitor crizotinib. Six years later, it was approved, thanks...
Read article

April 29, 2022
An Interview with Gabriel Tremblay on his Poster Contributions to ISPOR US 2022
At ISPOR US 2022, Cytel’s HEOR & RWE experts will be contributing to a range of Issue Panels, In-person Podium...
Read article

April 27, 2022
Reinventing Clinical Trial Design: Digital Development
New medicines and devices under development live and die on the strength of their clinical data. An asset’s journey is...
Read article

April 25, 2022
Insights on the New ADaM guidelines and Europe Interchange 2022
I am excited to see you all at the CDISC Europe Interchange, April 27 – 28 but unfortunately, it will be a virtual...
Read article

April 22, 2022
Cytel’s Single Arm Trials Panel Selected as a Part of ISPOR 2022
This past decade has undoubtedly witnessed an increase in the number of single arm trials submitted to HTA bodies....
Read article

April 21, 2022
Bayesian Statistics and Its Applications: New Webinar by Professor Yuan Ji
Sophisticated Bayesian Methods are gaining a lot of traction as they bring flexibility and speed to clinical trial...
Read article

April 13, 2022
Join Cytel’s HEOR Consultants at ISPOR US 2022
The Life Sciences landscape has seen an impactful digital evolution in the past two years. The pandemic has accelerated...
Read article

April 12, 2022
Career Perspectives: Interview with Charles Warne, Associate Director of Biostatistics
In this edition of the Career Perspectives series, I interview Charles Warne, Associate Director of Biostatistics at...
Read article

April 8, 2022
Robust Trial Design Under Treatment and Enrollment Uncertainty
The planning and optimization of a clinical trial is beset by uncertainties: knowledge of treatment effects, the...
Read article

April 7, 2022
Bridging the gap between oncology clinical trials and real-world data: evidence on replicability of efficacy results using German claims data
Randomized control trials (RCTs) are the gold standard for estimating the efficacy of a treatment. They allow us to...
Read article

April 5, 2022
Time Check: Developing New Therapeutics
Hello! I’m delighted to pen my inaugural blog post here as Cytel’s Chief Medical Officer. In this series, we’ll explore...
Read article

April 1, 2022
A Spotlight on Our Scientific Community
At the end of every year, scientists from across Cytel’s business units are nominated for Cytel’s Spotlight Awards,...
Read article

March 23, 2022
How to Use Historical Data to Mitigate Clinical Trial Risk
For over a decade, the number one reason cited for trial discontinuity has been challenges associated with recruitment...
Read article

March 18, 2022
The Fundamentals of Real World Evidence in Oncology Drug Development
Real world evidence (RWE) provides a large and growing source of insights into drug uptake and safety. It is...
Read article

March 11, 2022
WINTER WEEKEND READ: Increased Adoption of Innovative Designs
Every year, sponsors hesitating to use a complex innovative clinical trial design routinely miss opportunities to...
Read article

March 8, 2022
How to conduct better time-to-event analysis with delayed treatment effects
The issue of delayed treatment effects in immuno-oncology was demonstrated during a FDA-Industry sponsored workshop...
Read article

February 22, 2022
How and Why to Implement Optimal Adaptive Promising Zone Designs
When determining the best possible statistical design for a particular trial, large pharmaceuticals and small biotechs...
Read article

February 18, 2022
WINTER WEEKEND READ: Role of Data Strategy in Clinical Development Success
Data is the most crucial asset of any clinical trial and hence, sponsors cannot jeopardize collecting clean...
Read article

February 17, 2022
A Data Manager’s Role in Supporting a Rare Disease Clinical Study
It is a common perception that the role of a Data Manager is only to perform what we call “Data Cleaning”; making sure...
Read article

February 15, 2022
Measuring Estimates and Confidence Intervals in Adaptive settings?
As the use of advanced and innovative clinical trial designs continue to rise, sponsors often wonder which estimation...
Read article

February 11, 2022
WINTER WEEKEND READ: Tops Tips and Tricks from the Good Data Doctor
Adopting data standards such as CDISC in the early phase of clinical drug development contributes to the consolidation...
Read article
February 9, 2022
How can an optimized data strategy support your clinical program?
Data is the cornerstone of any clinical trial and is used to ultimately drive the decision-making process related to...
Read article

February 4, 2022
WINTER WEEKEND READ: Model-Based Enrollment Forecasting
The ability to conduct data-driven and quantitatively rigorous feasibility studies, is often key to successful trial...
Read article

February 2, 2022
How to Overcome Common Challenges to Patient Recruitment Projections
For nearly ten years, suboptimal trial enrollment has been cited as a primary cause of clinical trial discontinuation....
Read article

January 27, 2022
Winners of The Promising Zone Quiz
As a part of Cytel’s 10 Year Anniversary of the Promising Zone Design, Cytel hosted a quiz on “Keeping the Promise” –...
Read article

January 26, 2022
Career Perspectives: Interview with Jessica Bhoyroo, Clinical Data Manager
In this edition of the Career Perspectives series, I interview Jessica Bhoyroo, Cytel Clinical Data Manager based in...
Read article

January 25, 2022
Watch out, the FDA Rejection Criteria are Now in Place
In this blog, I share some experiences we recently had during an FDA submission Cytel performed for a sponsor after...
Read article

January 21, 2022
How to Use and Interpret the Results of a Platform Trial
For our first Winter Weekend Read, Cytel presents How to Use and Interpret the Results of a Platform Trial, a JAMA...
Read article

January 20, 2022
Is Borrowing Outcomes from US or China the Future for Rare Conditions?
Limited patient populations resulting in small study sample sizes is a difficulty associated with the development of...
Read article

January 19, 2022
What’s Ahead for Clinical Trial Design?
The past two years have been transformative for Cytel. Most notably, the global COVID-19 pandemic unleashed an...
Read article

December 23, 2021
Year-End Roundup: Your Favorite Blog Posts of 2021
Cytel blogs bring you debate and discussion of the newest trends in statistics and quantitative strategy. In 2021, our...
Read article

December 20, 2021
Approaches in Adaptive Group Sequential Clinical Trials
The promising zone design is an adaptive design which allows for sample size re-estimation based on the results of an...
Read article

December 15, 2021
CDISC SDTM and ADaM: An Explosive 2021 Ending!
Recently, on November 29 I received an email from CDISC announcing an important update for both SDTM and ADaM CDISC...
Read article

December 14, 2021
Is Promising Zone Design Optimal?
In traditional clinical trial design, the sample size is often determined to detect the target treatment effect with...
Read article

December 8, 2021
Conditional Powers Vs Bayesian Predictive Power for Adaptive Sample Size Reassessment
Despite the debate in the scientific community on adaptive sample size reassessment (SSR), noteworthy developments have...
Read article

December 7, 2021
Anna Forsythe on Aligning Clinical Strategy with Regulatory and Market Objectives
Sponsors bringing a successful new product to market have to overcome two hurdles: submission and reimbursement. For...
Read article

November 30, 2021
The FDA “Real-Time Oncology Review” Process
The FDA “Real-Time Oncology Review (RTOR)”[1] is an “FDA project started in 2018 to facilitate earlier submission of...
Read article
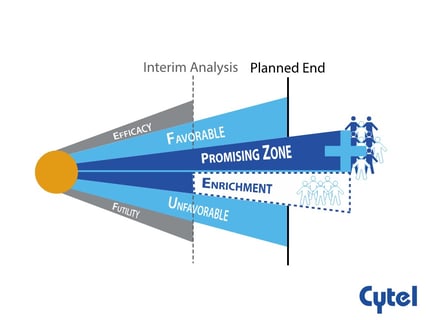
November 30, 2021
Dr. Julia Edwards Findings Promising Zone Designs
The aim of any clinical research is to detect the actual difference in treatment effect between two groups (power) and...
Read article

November 23, 2021
Using Single Arm Trials for HTA Submissions: Dr. Heeg and Maria Rizzo
A randomized clinical trial (RCT) is the gold standard approach to demonstrate the efficacy and safety of novel...
Read article

November 17, 2021
Using Tech to align Regulatory and Market Access Evidence strategies
Traditionally, the teams responsible for clinical development and regulatory submissions do not consult the market...
Read article

November 15, 2021
Optimal Promising Zone Designs: What Biotechs Need to Know
Since its first publication ten years ago, Cyrus Mehta and Stuart Pocock’s Promising Zone Design for sample size...
Read article

November 11, 2021
Championing RWE & HEOR at Virtual ISPOR Europe 2021
The value of Real World Evidence (RWE) is well known to many stakeholders, but its full potential for market access and...
Read article

November 10, 2021
Evolving the Study Design Process: An ACT Webcast by Dr. Yannis Jemiai
There are many reasons why traditional approaches to designing a clinical study are generally suboptimal and do not...
Read article

November 8, 2021
Keeping the Promise: Ten Year Anniversary of the Promising Zone Design
Ten years ago Cytel co-founder Professor Cyrus Mehta and Professor Stuart Pocock of the London School of Hygiene and...
Read article

November 4, 2021
Join Cytel for HEOR Insights at ISPOR Europe 2021
The prominent European conference for Health Economics and Outcomes Research (HEOR), ISPOR Europe 2021, is around the...
Read article

November 2, 2021
Empowering Trial Selection: An ACT Webcast by Dr. Yannis Jemiai
A good clinical study design performs well not only under the ideal target scenario. Statisticians should be able to...
Read article

October 29, 2021
Designing Platform Trials
A platform trial, a type of Master Protocol, is an experimental infrastructure to evaluate multiple treatments and/or...
Read article

October 27, 2021
Leveraging Staged Investment Strategy for Funding Novel Therapies
A staged investment strategy aligns R&D decisions and financial planning with the interim looks of a clinical trial. If...
Read article

October 22, 2021
The Benefits of Using Basket Studies in Oncology
Currently, there are many treatment options for Cancer such as, Immunotherapy, Radiation Therapy, Chemotherapy etc. If...
Read article

October 21, 2021
Measuring Non-Adherence and Non-Persistence
A number of methods currently exist to measure non-adherence and non-persistence of medical therapies, for improved...
Read article

October 20, 2021
Strategic Clinical Trial Design Unlocks Innovative Opportunity
For health innovators, trial selection is a key success factor as there are no second chances. But how do you find the...
Read article

October 15, 2021
Applications of Master Protocols in a Global Health Context
Almost 3000 registered trials were performed in COVID-19 and a majority of them have been small and likely...
Read article

October 14, 2021
Weighting and Prioritization for Trial Selection: New Webinar
When choosing the optimal clinical trial design for a given study, sponsors face critical questions like choice of...
Read article

October 7, 2021
Non-adherence and Non-persistence
‘Drugs do not work in patients who do not take them,’ said former surgeon general C. Everett Koop. Unfortunately, the...
Read article

October 6, 2021
The Rapidly Evolving Need for Master Protocols
Master Protocols are advanced and innovative clinical trial designs that can evaluate multiple therapies and disease...
Read article

October 5, 2021
The Importance of Traceability
Traceability is crucial in all steps of clinical data handling, from data collection to final analysis. The importance...
Read article

October 1, 2021
Dr. Kyle Wathen talks about the Need for Statistical Innovation
The COVID-19 pandemic elevated the challenge of designing and executing clinical trials within a substantially...
Read article

September 30, 2021
Transportability Analysis - An interview with Miguel Hernán
A complex methodological issue which arises in the production of real-world evidence involves the degree to which...
Read article

September 29, 2021
How to leverage model-informed drug development for rare diseases
While there is a plethora of rare diseases, some 7000 diseases and counting, one needs to consider the statutory...
Read article

September 24, 2021
ICT Magazine Interviews Dr. Yannis Jemiai on the Benefits of Bayesian
We may be familiar with adaptive designs, but their complexity has made them difficult to implement and their benefits...
Read article

September 23, 2021
Transportability Analysis - An interview with Professor Miguel Hernán
A complex methodological issue which arises in the production of real-world evidence involves the degree to which...
Read article

September 21, 2021
Three Underappreciated Benefits of Pareto for Empowered Trial Selection
Earlier this summer, we published a series of articles on the need to utilize weighting and prioritization tools in the...
Read article

September 15, 2021
A Bayesian Optimal Design Advancing the Precision Medicine Approach
There is recognized heterogeneity within any given tumor‐type from patient to patient (inter‐patient heterogeneity),...
Read article

September 14, 2021
Career Perspectives: Interview with Alyssa Biller, Senior Solutions Consultant
Alyssa Biller is a Senior Solutions Consultant at Cytel and currently plays a primary role in onboarding customers for...
Read article

September 8, 2021
Reconciling an old debate with modern technology
A key decision in the design of clinical trials in oncology involves whether to select progression free survival (PFS)...
Read article

August 31, 2021
CDISC Certification - is it worth taking?
For years, I have been telling the recruiters at Cytel to be wary of candidates claiming to have a CDISC Certification...
Read article

August 20, 2021
Using Causal Inference for Decision Making
In clinical research, decision makers need to choose among different courses of action every day. Whether it is...
Read article

August 18, 2021
What does reducing the risk of a faulty conclusion mean: Case study
During the design of a clinical trial, many biotechs want to substantially reduce the risk of a good new therapy being...
Read article

August 13, 2021
Finding the Optimal Trial Design Using Operations Research Methods
With the cloud computing power that we have today, we can run simulation of 1000s of designs with each design...
Read article

August 10, 2021
CLRPerm: Cytel Scientists and Collaborators Propose a New Method for Meta-analysis for Rare Events
A few weeks ago I wrote about new research conducted by Cytel statisticians, on the challenge of conducting...
Read article

August 9, 2021
When to make decisions? Strategic planning of interim looks.
Recently we discussed examining clinical development through a Bayesian lens, in honor of Cytel co-founder Nitin Patel...
Read article

August 5, 2021
Establishing the Comparative effectiveness and Safety of New Treatments Using Real World Data
It is important to compare competing interventions to determine value of medicines, both from clinical and societal...
Read article

July 30, 2021
In a Virtual Room with the FDA Reviewers
I had recently (for the first time) the pleasure and honor to attend a virtual meeting with the FDA, a pre-NDA Type-B...
Read article

July 28, 2021
Lessons Learned from Leveraging Computing Power for Clinical Strategy
“We found an optimal design in hours that might have taken months to find using standard methods,” reflected Fabien...
Read article

July 27, 2021
Thinking of Clinical Development from a Bayesian Lens
Program and portfolio optimization creates a framework throughout the course of the clinical development journey, that...
Read article

July 22, 2021
The Risk of Under-exploring Trial Design Options: A New Case Study
Earlier this year, Cytel founder Cyrus Mehta observed that clinical trial design is often treated like an art rather...
Read article

July 21, 2021
Bayesian Approach to Benefit-Risk Assessment
Conducting a transparent, targeted and robust benefit-risk assessment of a new drug or product is one of the most...
Read article

July 20, 2021
Career Perspectives: Interview with Anil Golla, Vice President, FSP
Anil Golla is Vice President, Functional Service Provision (FSP) at Cytel. After 17 years of working at pharmaceutical...
Read article

July 14, 2021
Novel Uses of Scoring Functions in Clinical Trial Design Selection
For decades, statisticians have cultivated methods to optimize and de-risk clinical trials for strong regulatory...
Read article

July 12, 2021
Using Confidence Distributions to Manage Statistical Heterogeneity
Medical researchers and public health experts are becoming more reliant on meta-analyses to capture in summary form,...
Read article

July 7, 2021
Ensuring You Get Optimal Study Power for Your Investment
Suppose a statistician were to tell a clinical trial sponsor that it was possible to improve the power of the sponsor’s...
Read article

July 2, 2021
Use of Rolling-enrollment Designs to Accelerate Clinical Trials
Popular statistical designs, such as CRM (O’Quigley et al., 1990), mTPI-2 (Guo et al., 2017), and i3+3 (Liu et al.,...
Read article

July 1, 2021
Myths surrounding the use of synthetic control arms in clinical trials: Part 4
Synthetic control arms (SCAs) are best suited for situations when a single arm trial is run in a patient population...
Read article

June 30, 2021
Mathematical Methods for Clinical Trial Financial Strategy
When Cyrus Mehta introduced the Promising Zone Design over a decade ago, the new statistical method not only...
Read article

June 25, 2021
Leveraging External Data for Efficient Trial Designs
The main challenge associated with the development of therapies for rare diseases is typically the small study sample...
Read article

June 24, 2021
Myths surrounding the use of synthetic control arms in clinical trials: Part 3
Synthetic control arms (SCAs) leverage real world data from various sources or evaluations of historical clinical data...
Read article

June 23, 2021
Eliminating Underperforming Clinical Trial Designs
Much of the discussion about clinical trial design considers methods to optimize performance characteristics and...
Read article

June 18, 2021
Use of Scoring Functions for Clinical Trial Optimization
Next week’s PSI Conference will feature Dr. Yannis Jemiai speaking on the use of Scoring Functions in the re-imagined...
Read article

June 17, 2021
Myths surrounding the use of synthetic control arms in clinical trials: Part 2
In Part 2 of this four-part blog series, we bust another myth surrounding synthetic control arms (SCAs) used in...
Read article

June 15, 2021
The Promising Zone Ten Years Later
Ten years ago, a seminal paper published by Cytel Founder Cyrus Mehta, introduced the Promising Zone Design to...
Read article

June 14, 2021
Practicalities of Integrating Electronic Health Records into Data
ACDM’s (Association for Clinical Data Management) eDigital data management expert group (DMEG) focuses on driving...
Read article

June 10, 2021
Myths surrounding the use of synthetic control arms in clinical trials: Part 1
Over the past decade, single arm trials have emerged as an accepted way of assessing a new treatment intervention....
Read article

June 9, 2021
Selecting a Clinical Trial Design: How Broadly Should You Explore?
When selecting clinical trial designs, how many design options should a sponsor explore? Would a sponsor feel more...
Read article

June 4, 2021
Bayesian Methods: Paving the path to Clinical Development Transformation
Bayesian methods have been playing a key role in transforming clinical research in therapeutic areas such as oncology...
Read article

June 3, 2021
Information Borrowing in Basket Trials
Bayesian methods allow for the incorporation of prior knowledge, in terms of either expert opinion from clinicians or...
Read article

June 2, 2021
A Data-Infused Approach to De-Risking Clinical Trials
For many decades the Pareto Frontier has been employed by actors in the private sector to evaluate and understand the...
Read article

May 28, 2021
Use of Bayesian Approach in Basket Trial Design
Advancements in biomarkers and momentum in precision medicine has paved the foundation for complex studies like basket...
Read article

May 21, 2021
Use of Bayesian Analysis in Platform Trials: Webinar by Dr. Kyle Wathen
Most of us are familiar with the concept of platform clinical trials as they have gained popularity in the recent...
Read article

May 20, 2021
Quantitative Bias Analysis to Strengthen Comparative Effectiveness
As more payers and HTA agencies turn to real world data to compare the effectiveness of various treatment effects, two...
Read article

May 19, 2021
A Non-Technical Guide to Statistically-Informed Clinical Strategy
Clinical trial sponsors are more likely than ever to use the power of simulation and forecasting to evaluate the...
Read article

May 14, 2021
Starting the Conversation Early: Incorporating Business Considerations in Optimal Selection of Trial Design
When developing clinical strategy, applying familiar business principles to the specific requirements of clinical...
Read article

May 13, 2021
An Interview with Radek Wasiak, Head of Real World and Advanced Analytics at Cytel
Cytel’s HEOR and RWE Expertise has grown quite significantly in the past year. Could you speak a little bit about the...
Read article

May 12, 2021
Strategic Insights from Novel Bayesian Methods – Complimentary Paper
Did you know that Bayesian methods can strengthen Frequentist trials through the use of Bayesian decision criteria or...
Read article

May 7, 2021
Never Miss the Optimal Study Design Options
When is a study design considered to be optimal? A good design performs well not only under the ideal target scenario...
Read article

May 5, 2021
Meet our Global HEOR and RWE Experts: Virtual ISPOR 2021
Cytel’s team of HEOR and Real-World Evidence (RWE) experts are all set to make a splash at the Virtual ISPOR on May 17...
Read article
May 4, 2021
New Publication on Adaptive Platform Trials
As healthcare systems across the world, continue to grapple with the pressures of COVID-19, Cytel advances yet another...
Read article

April 29, 2021
Advances in HEOR: An Interview with Anna Forsythe
After twenty years in pharma, Anna Forsythe was frustrated by traditional vendors who used outdated methods to prepare...
Read article

April 28, 2021
Trial Selection: From Art to Science
Recently, Cytel co-founder Professor Cyrus Mehta noted that, “Clinical trial design selection is too much like an art,...
Read article

April 26, 2021
Why you should not miss 2021 Virtual CDISC EU Interchange?
As we all continue to take necessary precautions against the spread of COVID-19 virus, this year again the CDISC EU...
Read article

April 23, 2021
Bayesian Methods & Vaccines Research: COVID-19
The urgent need to discover and assess the efficacy and safety of COVID-19 vaccine candidates will affect the future...
Read article

April 21, 2021
Understanding Head-to-Head Clinical Trials
Two therapies are placed in head-to-head clinical trials when they are compared against each other as opposed to a...
Read article

April 20, 2021
New Dimensions of Clinical Trial Optimization
For much of the past three decades, even as methodologies for clinical trial design have advanced and refined, the idea...
Read article

April 14, 2021
Reaping the Benefits of Bayesian Innovation
In the era of modern clinical development, several companies are turning towards novel and innovative approaches such...
Read article

April 13, 2021
7 Steps to an Evidence Dossier for Wearables
There has been an increasing use of digital measures in drug development recently. New wearables technologies can help...
Read article

April 7, 2021
Career Perspectives: Interview with Neha Sati
Scientists at Cytel recently published a paper in the Journal of the American Medical Association (JAMA). Among the...
Read article
April 2, 2021
Using Bayesian Networks to Predict Survival Outcomes: New Case Study
Earlier this month, my colleagues at Cytel Canada published a paper in JCO Clinical Cancer Informatics, offering a...
Read article

March 31, 2021
Wearables and Decentralization
As decentralized clinical trials become more attractive in an era of COVID-19, the role of wearables in clinical...
Read article

March 30, 2021
The Integration Dilemma
As of today, our Industry has not defined any approach, nor does an official regulatory agency...
Read article

March 26, 2021
Using External Evidence for Decision-Making for Medical Devices
Former Commissioner of the FDA, Dr. Scott Gottlieb, in several public presentations, would bemoan missed chances to...
Read article

March 25, 2021
US Regulatory Aspects of Wearable Medical Devices
Wearables have experienced increasing applicability within medical device trials, yet the regulations for the use of...
Read article

March 19, 2021
5 Steps to Regulatory Success with Wearables Designs
The use of wearable and digital technology requires considerations for both drugs and devices regulations, and...
Read article

March 18, 2021
Computing & Statistics: Are You Ready for the Industry Transformation?
Over the past ten years High-Performance Computing (HPC) has transformed medical research through advances in genomics,...
Read article

March 12, 2021
Wearables: Translating raw data to actionable information
With wearables likely to become a regular part of clinical trial design, statisticians could benefit by familiarizing...
Read article

March 11, 2021
Data and analysis in Modern Oncology Clinical Development
In the recent years, Oncology trials are seeing a technological shift that is expected to make them faster and more...
Read article

March 9, 2021
Seeing Uncertainty: New Frontiers of Statistical Communication
When statistical sciences were in their infancy, the communicative benefits of statistics were widely touted. Thousands...
Read article

March 5, 2021
Single Arm Multi-Stage Phase 2 Cancer Trials
Early stage Phase 2 clinical trials are often designed as multi-stage single arm trials, which quickly identify...
Read article

March 2, 2021
Hybrid Bayesian and Frequentist Clinical Trial Designs
Most people know that clinical drug discovery is usually conducted using either Frequentist or Bayesian methods. These...
Read article
February 26, 2021
Empowering Statisticians to Create Complex Bayesian Clinical Study Designs
In the world of clinical trials, the pace of innovation is accelerating, and approaches such as Bayesian methods are...
Read article

February 25, 2021
Use of Wearables in Confirmatory Clinical Trials
The convergence of several distinct trends has made wearables an increasingly attractive option for use in confirmatory...
Read article

February 24, 2021
Avoiding Lost-in-Translation with Submission Terminology
In a previous post, I discussed the importance of proper use of CDISC Controlled Terminology (CDISC CT) in SDTM....
Read article

February 19, 2021
Selecting Your Next Clinical Trial Design Using Quantitative Methods
C-Suite and R&D Decision-Makers are always striving to make evidence-driven decisions. Yet the rules by which evidence...
Read article

February 18, 2021
Introduction to Evidence Synthesis and Bayesian dynamic borrowing
In the last few years, there has been a growing interest in historical borrowing or augmented trials. There is an...
Read article
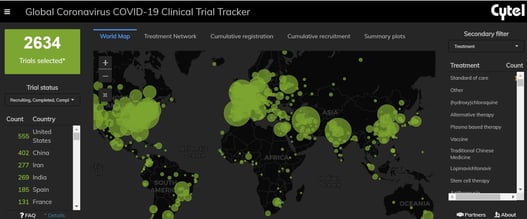
February 17, 2021
An Interview with Louis Dron on the Benefits and Future of Cytel’s Trial Tracker
The COVID-19 Pandemic prompted the rapid surge in the generation of clinical data that has been scattered across...
Read article

February 12, 2021
Leveraging Synthetic and External Control Arms Using Bayesian Methods
In recent times, Single arm trials are being increasingly used to assess new treatment interventions. They establish...
Read article

February 11, 2021
The biostats and clinical overview of a growing clinical strategy
The past two years have witnessed a heightened interest in the use of wearables in clinical development. The unexpected...
Read article

February 9, 2021
New Meta-Analysis in JAMA Uses Novel Quantitative Techniques to Demonstrate Baseline Characteristics Informing Response to Common Therapy for Kidney Cancer
Recent years have witnessed improving survival outcomes for those struggling with a range of common kidney cancers....
Read article

February 4, 2021
Simulation Based Clinical Trial Optimization
The past decade has witnessed the rise of simulations-based clinical trial optimization in a manner unimaginable to...
Read article

February 2, 2021
Bayesian Methods for Master Protocols
As the use of master protocols becomes more prevalent in drug development, Bayesian methods are extensively used to...
Read article
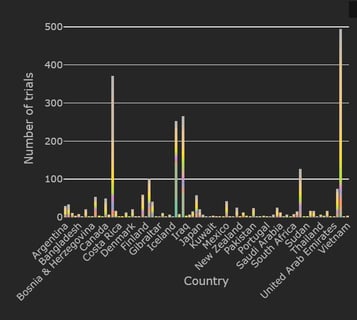
February 1, 2021
February 2021: Updates from the CYTEL COVID-19 Trial Tracker
Cytel’s COVID-19 Trial Tracker continues to provide real time updates to the status of COVID-19 clinical trials...
Read article

January 29, 2021
Computation and Clinical Trial Design: New Directions
Historically, advances in the statistical design of clinical trials have accompanied progress within the science and...
Read article

January 28, 2021
A little walk in the CDISC Library, hand in hand with SAS
The Christmas break presented an opportunity to make my first concrete steps into the CDISC Library. Overall, it was a...
Read article

January 26, 2021
Cytel Thought Leadership on Power of Bayesian Methods
Bayesian models offer a flexible way of incorporating historical controls in the analysis of trial data (whether single...
Read article

January 22, 2021
The Role of Real World Evidence after COVID19
COVID-19 has transformed the pharmaceutical industry in a manner that few could have predicted only a year ago. One of...
Read article

January 20, 2021
Quantifying Tradeoffs in Clinical Development
One of the most difficult challenges facing Research and Development teams involves determining how to make tradeoffs...
Read article

January 19, 2021
Cytel COVID Panel: Long-term Changes to Clinical Trials Due to the Pandemic
As we enter 2021 with new COVID-19 vaccines and greater optimism about the pipeline of drugs and devices positioned for...
Read article

January 13, 2021
How to Create a High-Quality Globally Distributed Biometrics Team?
Effective use of the right outsourcing solution can enable sponsors to respond to market needs and change course where...
Read article
January 12, 2021
5 Questions to Help You Modernize Clinical Development
The rapid pace of technology has opened up numerous avenues for advanced innovative clinical trial design, but how can...
Read article
January 11, 2021
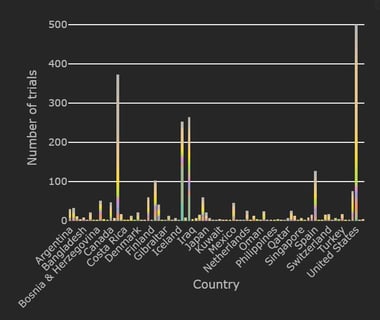
COVID-19 Trial Tracker Updates (January 11)
In April 2020, Cytel launched an open-access global COVID-19 Clinical Trial Tracker to help facilitate greater...
Read article

December 22, 2020
Year-end Roundup: Cytel’s Contributions Towards Health & Education in 2020
At Cytel, we have been diligently working to become an organization deeply committed to uplifting and enriching...
Read article

December 21, 2020
Year-End Roundup: Your Favorite Blog Posts of 2020
2020 has been an unusually difficult year as the global pandemic impacted all of our lives. This year, the Cytel blog...
Read article

December 18, 2020
Submitting Software Programs to the Regulatory Agencies
Can I submit software programs other than SAS? What software programs should I submit? Are sponsors required to submit...
Read article

December 17, 2020
2020 Recap by Yannis Jemiai, Chief Scientific Officer, Cytel
As Chief Scientific Officer, Dr. Yannis Jemiai plays a pivotal role in maintaining Cytel’s well-established reputation...
Read article

December 16, 2020
2020 Recap by Pantelis Vlachos, Principal/Strategic Consultant, Cytel
As we prepare to close the door on 2020, we asked Pantelis Vlachos, Principal/Strategic Consultant for Cytel, to share...
Read article

December 15, 2020
Satisficing, Optimizing and Globally Optimizing Trial Designs
When designing clinical trials, biostatisticians and clinical development teams are often faced with a conundrum. Given...
Read article

December 10, 2020
Career Perspectives: Interview with Sachin Sobale
Sachin Sobale began his career with Cytel as a young statistician. He has been associated with the company for more...
Read article

December 9, 2020
7 Key Features of Strategic Clinical Trial Design
As a part of Cytel’s Advanced Design Framework, a new Framework for the statistical design of clinical trials, Cytel...
Read article
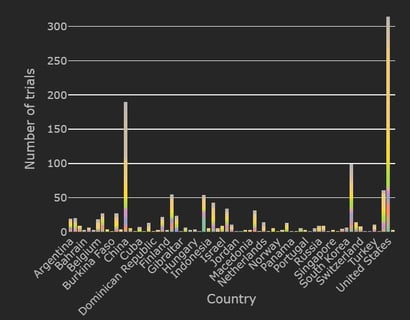
December 8, 2020
COVID-19 Trial Tracker Updates (December 8)
The Cytel COVID-19 Trial Tracker brings you an up to the minute, real time dashboard about COVID-19 trials around the...
Read article

December 3, 2020
New Whitepaper: Reimagining Clinical-Trials
Increasing Clinical Development Productivity Using Statistics and Cloud-Computing The need for Re-imagining Clinical...
Read article

December 2, 2020
Program and Portfolio Optimization: A New Paradigm
Significant advances have been made to enhance the efficiency of clinical trial designs. However, the traditional...
Read article
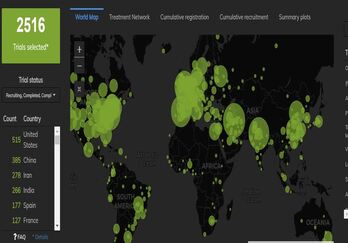
December 1, 2020
Mapping the Landscape of COVID-19 Clinical Trials in the US
An extraordinary amount of global research is underway as the COVID-19 pandemic continues to evolve and spread. As...
Read article

November 24, 2020
Cytel and Ingress Health at Virtual ISPOR Europe 2020
Virtual ISPOR 2020, held November 16 to 19, presented new opportunities for scientific interaction amongst HEOR...
Read article

November 23, 2020
Data Standards and Submission Highlights from PHUSE EU CONNECT 2020
The Virtual PHUSE-EU CONNECT Conference was held from November 8 to 13 and the event was a great success, despite all...
Read article

November 19, 2020
10 Key Qualifications for Independent Statisticians Reporting to the DMC
Data Monitoring Committees (DMCs) are groups of independent experts who periodically receive (by-arm) reports created...
Read article

November 18, 2020
We can design over 100,000 clinical trials in less than an hour
The current state of the clinical trials industry faces a challenge that was only hypothetical three or four years ago....
Read article
November 17, 2020
Role of Prediction and Causal Inference in Clinical Research
As a part of Cytel’s "New Horizons Webinar Series", Alind Gupta, Senior Data Scientist, presents case studies from his...
Read article

November 16, 2020
Bayesian Methods for Multiple Cohort Expansion (MuCE) designs
MUCE is a Bayesian solution for cohort expansion trials where multiple dose(s) and multiple indication(s) are tested in...
Read article

November 12, 2020
Join Cytel and Ingress Health at Virtual ISPOR Europe 2020
Cytel and Ingress Health (now a Cytel company) will be contributing to a range of events at Virtual ISPOR EUROPE 2020,...
Read article

November 11, 2020
Interview with Yannis Jemiai: Advanced Design Framework
The widespread use of cloud-computing has altered the clinical trial design process. Whereas three or four years ago,...
Read article
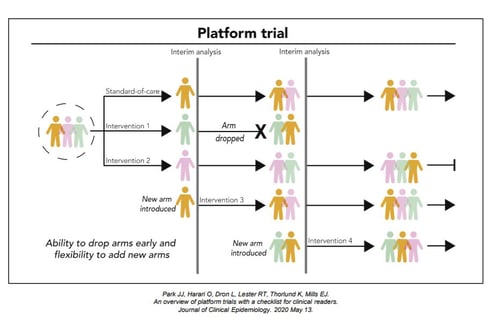
November 10, 2020
Key Design Considerations for Platform Trials
Platform trials are a new type of clinical trials where multiple interventions can be evaluated simultaneously against...
Read article
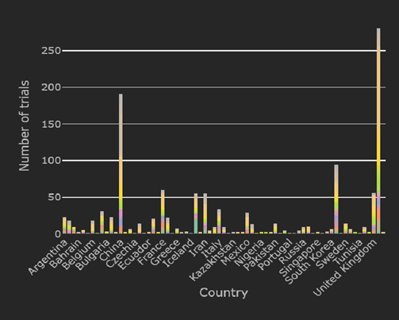
November 9, 2020
COVID-19 Trial Tracker Updates (November 9)
As the evolving COVID-19 pandemic continues, the Cytel COVID-19 Trial Tracker continues to bring you an up to the...
Read article

November 5, 2020
Role of RWA in Transforming Oncological Research
In oncology, many manufacturers go into niche indications, where there are very specific tumors, and then they opt for...
Read article

November 4, 2020
Cytel Introduces Advanced Design Framework: Part 3 - Communication Techniques to Ensure Alignment on Data-Driven Clinical Trial Designs
Cytel has recently revealed its Advanced Design Framework, a method developed by Cytel’s thought leaders that draws on...
Read article

November 3, 2020
Staffing Needs for RWE Delivery
When an expert statistician is paired with an experienced set of data managers, opportunities to capitalize on...
Read article

November 2, 2020
Value of Detailed Clinical Trial Simulations for Rare Diseases
Measuring treatment effect during a clinical trial is often the source of much debate, particularly during rare disease...
Read article

October 29, 2020
Advanced Design Framework: Part 2 - A Quantitative Evaluation Approach
Cytel has recently revealed its Advanced Design Framework, a method developed by Cytel’s thought leaders that draws on...
Read article

October 28, 2020
When your ADaM package is not traceable back to SDTM
About three years ago, Cytel was helping a sponsor on a project where I had to conduct surveillance of some CRO...
Read article

October 27, 2020
Bayesian Dose-Finding Designs – An Overview
Cytel recently conducted a webinar on Bayesian Dose-finding Designs for Modern Drug Development, presented by Dr. Yuan...
Read article

October 26, 2020
Need for Technology Solutions to Support Computationally
Pharmaceutical and biotech companies are under pressure to deliver more and deliver faster with fewer resources. The...
Read article

October 23, 2020
Yuan Ji on U-Design: An All New Efficacy and Toxicity Dose-Finding Module
Cytel’s New Horizons Webinar Series introduces you to the latest innovations in statistical trial design. This webinar...
Read article

October 22, 2020
An Interview with Bart Heeg (Part 2): New Trends in HEOR
In this two-part blog series, we interview Bart Heeg, Vice President HEOR and Founder at Ingress Health (A Cytel...
Read article

October 21, 2020
Advanced Design Framework: Part 1 - Exploration of Design Space
Cytel has recently revealed its Advanced Design Framework, a method developed by Cytel’s thought-leaders after a decade...
Read article

October 20, 2020
Interview with Thomas Wilke: Health Economics/World Evidence Studies
In this interview with Thomas Wilke, Principal Scientist at Ingress-Health (a Cytel company), we talk to him about his...
Read article

October 19, 2020
The Uniqueness of COVID-19 Data Challenges; The COVID-19 trial tracker
COVID-19 has created extreme uncertainties -- a dearth of historical information combined with the need for safety,...
Read article

October 15, 2020
An Advanced Design Framework for Clinical Development in the Era of Cloud-Computing
For over a decade, advanced trial design techniques have promised efficient trials with accelerated timelines,...
Read article

October 14, 2020
The Increasing Importance of Health Economics
A credible evidence base is needed to support and document the economic value of new technologies and therapeutic...
Read article
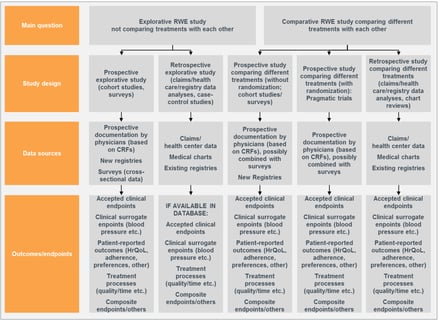
October 13, 2020
Introducing Observational Studies – Three Trends for Statisticians
The combination of greater access to electronic health records, bigger electronic claims datasets, and the need for...
Read article

October 12, 2020
Bayesian Statistics and FDA Regulatory Acceptability
Cytel and Novartis are together hosting a complimentary Bayesian Virtual Symposium and an Interactive 7-part workshop....
Read article

October 9, 2020
Cyrus Mehta on Increasing the Power of Platform Trials
Even before the era of COVID-19, significant attention was channeled to the overwhelming potential of adaptive MAMS...
Read article

October 7, 2020
RWE Needs for Natural History Studies
With the rise in digital technologies, there has been an explosion in the volume and type of data sources. We can...
Read article

October 5, 2020
The Meta-Analytic-Predictive Priors Generation and Comparisons
Staying abreast of the rapid pace of clinical development means adopting innovative or computationally intensive...
Read article
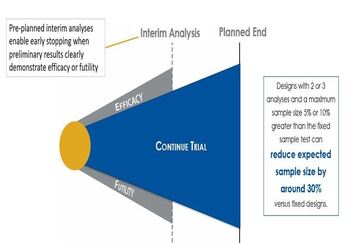
October 1, 2020
Improve Trial Design with Sequential Design and Sample Size
Methods involving Group Sequential Designs are one of the earliest deviations from a traditional two-arm clinical trial...
Read article

September 30, 2020
A Virtual Event Brought to you by Cytel and Novartis on Innovations
Today, there is a need for advanced quantitative techniques to combine all available information for better decision...
Read article

September 29, 2020
The New Horizons Series: Adaptive Multi-arm Multi-stage Clinical Trials
Innovation in trial designs are offering new routes forward for organizations of any size. They are now also aligned...
Read article

September 28, 2020
Advantages of platform designs for investigating COVID-19 therapies
Cytel has recently designed and implemented the TOGETHER Trials, funded by the Bill & Melinda Gates Foundation to...
Read article

September 25, 2020
Use of External Controls in Clinical Development – Download Audiobook
Regulators in both the United States and Europe have responded positively to the use of synthetic control arms (SCA)s...
Read article

September 22, 2020
LIBERTY claim analysis manuscript by Thomas Wilke and Sabrina Mueller
Research Scientists, Thomas Wilke and Sabrina Mueller recently published a manuscript on “Diabetes-Related...
Read article

September 21, 2020
Novel Adaptive Platform Trial for COVID-19 Therapies
Cytel has designed and implemented a novel adaptive platform trial for early stage COVID-19. The severity of the...
Read article

September 17, 2020
East Alloy: Accelerating the pace of innovation
Keeping up with the rapid pace of clinical development means that we need to adopt the innovative or computationally...
Read article

September 16, 2020
New Audiobook on Synthetic Control Arms
Synthetic control arms (SCA) are virtual trial arms that use historical claims data and observational data to simulate...
Read article

September 15, 2020
Accurately analyze small, skewed or sparse data with StatXact
In clinical trials with small or sparse data, statistical methods meant for large sample sizes may not be helpful to...
Read article

September 14, 2020
From Before to After: Preparing and Concluding your FDA Data Submission
“A good start is half the battle” (the Before) when submitting data to the FDA and there are a couple of cherries to...
Read article

September 10, 2020
Does your Trial need a Synthetic Control Arm?
Single arm trials are emerging as an accepted way of assessing a new treatment intervention. They establish clinical...
Read article

September 9, 2020
Importance of Designing Clinical Trials from a Program Perspective
Cytel’s co-founder, Nitin Patel, conducted a webinar on designing clinical trials from a program-level perspective. His...
Read article

September 4, 2020
Cytel Co-Founder Cyrus Mehta Presents at the Heart Failure Collaboratory, a Public-Private Partnership with FDA
On Friday September 11, Cyrus Mehta, co-founder of Cytel, will be delivering a talk to the Heart Failure Collaboratory,...
Read article

September 1, 2020
FSP Navigator – Building the Team that Brings Success
In this blog, Cytel's SVP Corey Dunham’s talks about our Functional Services teams and the qualities we seek in new...
Read article

August 31, 2020
Adopt innovative and computationally intensive designs with East Alloy
Pantelis Vlachos, Principal, Strategic Consultant at Cytel, conducted a webinar to introduce the capabilities of East...
Read article

August 26, 2020
Career Perspectives: Interview with Yannis Jemiai, Chief Scientific Officer
As Chief Scientific Officer, Dr. Yannis Jemiai plays a pivotal role in maintaining Cytel’s well-established reputation...
Read article

August 25, 2020
Nitin Patel on Designing Clinical Trials from a Program Perspective
It is important to take a strategic approach to clinical development in order to minimize the potential for Phase 3...
Read article

August 21, 2020
Bayesian Borrowing and Real World Data: The Fundamentals
As uses of real world data become more familiar for trial design and regulatory submission, sponsors might become more...
Read article

August 19, 2020
Webinar on Adaptive Designs for Dose Finding: Part 2
Bjoern Bornkamp, Statistical Methodologist at Novartis and Jose Pinheiro, Senior Director, Johnson & Johnson provided...
Read article

August 18, 2020
Career Perspectives: Interview with Mrudula Joshi, Associate Director, Statistical Programming Services
Mrudula Joshi joined Cytel in July 2005 as a young SAS programmer. Last month, she celebrated her 15th year work...
Read article

August 13, 2020
Webinar: Adaptive Designs for Dose Finding
Bjoern Bornkamp, Statistical Methodologist at Novartis and Jose Pinheiro, Senior Director, Johnson & Johnson provided...
Read article

August 12, 2020
Virtual Careers Open Day at Cytel
Cytel’s Biostatistics and Statistical Programming team provides integrated solutions, by blending the expertise of...
Read article

August 11, 2020
Optimizing Information in Trial Design and Implementation
While there is increasing optimism about the discovery of a COVID-19 vaccine, one of the less talked about aspects of...
Read article

August 7, 2020
Creating a Synthetic Control from Your Natural History Study
Recently a biotech approached Cytel for support with a Phase 2 Study in oncology. Regulators had requested a natural...
Read article

August 5, 2020
Design and Data Considerations from Cardiovascular Pilot Investigation
Cytel is conducting two pilot projects on head-to-head comparisons using real world data. These projects in oncology...
Read article

August 4, 2020
Estimands and their Implications on Clinical Studies
Last year, Paul Terrill, Associate Principal of Strategic Consulting at Cytel, presented an engaging webinar on the...
Read article

July 30, 2020
Cytel Scientists Call for a “Statistician-First Workflow” to Optimize Drug Development
A new peer-reviewed article co-authored by several Cytel scientists re-examines the way in which adaptive trials are...
Read article

July 28, 2020
Therapeutic Area User Guidance – The hidden Gems
CDISC standards have been around for a while with the first SDTM Standard version released in 2004. However, it was...
Read article

July 27, 2020
Introduction to Population Enrichment by Dr. Thomas Burnett
Cytel is conducting a webinar series on complex innovative trial designs. Dr. Thomas Burnett, Senior Research Associate...
Read article

July 23, 2020
Why Consider a Synthetic or External Control Arm?
Just as there are numerous adaptations that fall within the umbrella of adaptive designs, there are several different...
Read article

July 22, 2020
Access Sustainable, Verified Innovation with East Alloy
Cytel brings to you a new blog series on technology and Bayesian decision-making by Pantelis Vlachos,...
Read article

July 21, 2020
Head to Head Comparisons Using Real World Data
Cytel is conducting a webinar series that focuses on target trial emulation and causal inference approaches using real...
Read article

July 15, 2020
Three Reasons Why Oncology Trials Need Clear Estimands
Unlike many therapeutic areas, oncology benefits from having standardized endpoints like overall survival and...
Read article

July 14, 2020
The FSP Engagement Landscape: Reducing Sponsor Oversight Burden
Cytel SVP Corey Dunham’s inaugural post on leading the industry’s largest Biometrics CRO considers the FSP Engagement...
Read article

July 13, 2020
Interview with Dr. Thomas Burnett on Adaptive Enrichment
Cytel is hosting a complimentary webinar series that introduces biostatisticians and other members of the development...
Read article
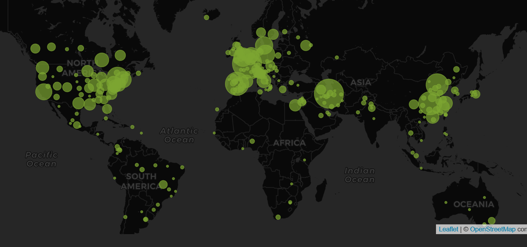
July 11, 2020
COVID-19 Clinical Development Quiz (with Answers)
Last week we challenged you to take a COVID-19 Clinical Development Quiz. Many of you used our Trial Tracker to find...
Read article

July 9, 2020
Synthetic control arms demystified: A Cytel Ebook
There has been an increased use of synthetic control arms for regulatory submissions in recent years, with three rare...
Read article

July 7, 2020
Overcoming Clinical Development Challenges in Oncology with Innovative
Having its roots in the seminar rooms of the Dana Farber Cancer Institute, Cytel has a long record of establishing new...
Read article
July 2, 2020
COVID-19 Clinical Development Quiz
There are currently 1570 registered clinical trials for COVID-19 therapies and vaccines. Approximately 20% are...
Read article

June 29, 2020
The Good Data Submission Doctor: CDISC for COVID-19
From the time the COVID-19 outbreak was declared a pandemic, the number of studies conducted around the world to either...
Read article

June 27, 2020
New Whitepaper: Bayesian Methodologies for COVID-19 Drugs
Expert statisticians at Cytel have spent the past three and a half months designing and deploying dozens of trials for...
Read article

June 24, 2020
Webinar - Practical Model-based Approaches for Phase I Oncology Trials
Last week, Cytel conducted its third webinar in the new introductory webinar series on Complex Innovative Trial...
Read article
June 23, 2020
Design and Data Source Considerations from Pilot Investigations in CVD
Supposing two treatments, A and B, need to be compared that have not been compared through a clinical trial. In the...
Read article

June 22, 2020
Webinar: Synthetic and External Controls in Clinical Trials
Cytel scientists recently published a new eBook on synthetic control arms and a new scientific primer for the more...
Read article

June 18, 2020
Why You Should Construct Primary Endpoints Using Bayesian Methods
One of the revelations of the COVID-19 pandemic is that the flexibility and potential of Bayesian designs goes far...
Read article

June 18, 2020
Optimizing Patient Recruitment: Download Whitepaper
A number of trials recently disrupted by the COVID-19 pandemic are now in the process of re-assessing recruitment...
Read article

June 15, 2020
Significance of Bayesian Model-Based Approaches in Oncology Trials: An Interview with Dr. Satrajit Roychoudhury
Cytel conducted a webinar with Dr. Satrajit Roychoudhury, Senior Director, Statistical Research and Data Science...
Read article
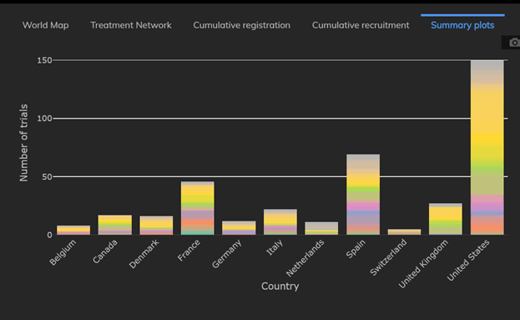
June 13, 2020
Weekly Updates from the COVID-19 Trial Tracker (June 12)
The Cytel COVID-19 Trial Tracker continues to bring you an up to the minute, real time dashboard about COVID-19 trials...
Read article
June 11, 2020
Adaptive Bayesian Methods: The Secret Weapon in COVID-19 Vaccine Development
A recent Cytel panel led by Vice President of Strategic Consulting Natalia Muhlemann evaluated the role that Bayesian...
Read article
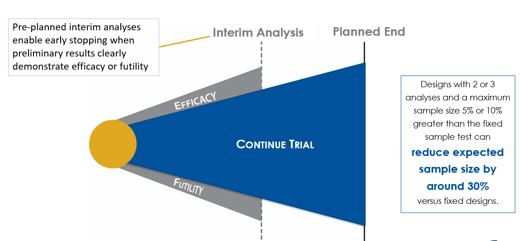
June 10, 2020
Group Sequential Designs and Sample Size Re-estimation
Cytel is conducting a webinar series that introduces biostatisticians to some of the more commonly used complex...
Read article
June 9, 2020
Melinda Gates, on COVID-19 and Drug Development in Emerging Economies
Trevor Mundel leads the Bill & Melinda Gates Foundation’s efforts to develop high-impact interventions against the...
Read article

June 8, 2020
New Primer and Ebook on Synthetic Control Arms
Cytel has recently published a new ebook on synthetic control arms, and a new scientific primer as well.
Read article
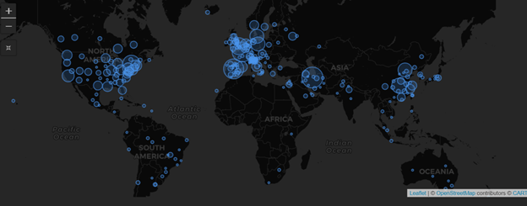
June 4, 2020
COVID-19 Weekly Brief
This weekly snapshot gives you a quick briefing on the state of COVID-19 therapy and vaccines development. As we head...
Read article
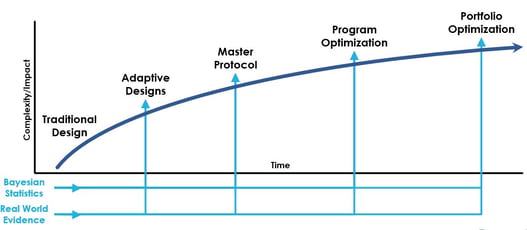
June 1, 2020
Webinar Replay: Innovative Drug Development at a Glance
In a recent interview with Cytel, Zoran Antonijevic, longstanding chair and leader of the DIA Adaptive Design...
Read article

May 29, 2020
Trial Tracker: State of COVID-19 Development (May 2020)
At the close of May 2020, we have about 500 new trials globally but trends in trial design and choice of therapies...
Read article

May 28, 2020
Implications for the Future of Drug Development in Emerging Economies
On May 7, Cytel and Certara conducted a virtual panel discussion on new opportunities and implications for the future...
Read article

May 27, 2020
Group Sequential Designs and Sample Size Re-estimation
In this blog, we speak with Christopher Jennison, Professor of Statistics at the University of Bath, UK. Professor...
Read article
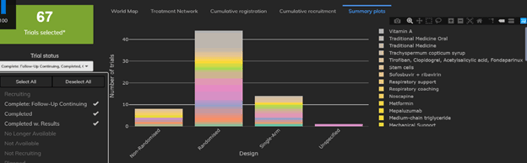
May 22, 2020
4 Things You Need to Know about COVID-19 Trial Designs
The Cytel Trial Tracker now features summary plots that display trials by country, trial status and study design. This...
Read article

May 18, 2020
Interview with Zoran Antonijevic on Adaptive Design Methods
In this blog, we speak with Zoran Antonijevic, longstanding chair and leader of the DIA Adaptive Design Scientific...
Read article
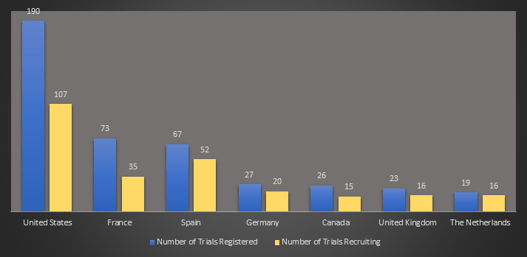
May 14, 2020
Weekly COVID-19 Trial Tracker Updates
This has been an exciting week for COVID-19 studies. We learned that several Cytel clients who have designed new...
Read article

May 12, 2020
Oncology Trial Design & Development Webinar Series
In our previous blog, “Remote Working Arrangement – How to get it right?”, we talked about how the need for social...
Read article
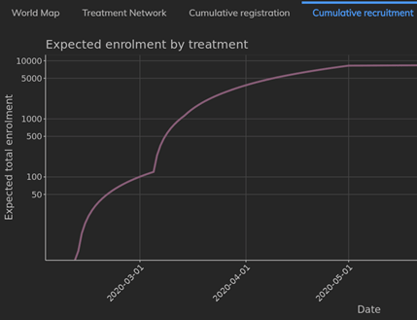
May 7, 2020
Weekly Insights from the COVID-19 Trial Tracker: Oxford Vacine Study
There are now over 950 trials registered, which means that 250 new trials were registered in the past week. Only 540 of...
Read article

May 7, 2020
COVID-19: Trials, Designs and Tools for Promising Results - A Virtual Panel Discussion
An extraordinary amount of global research is underway as the COVID-19 pandemic continues to evolve and spread...
Read article

May 5, 2020
Webinar: A Clinician’s Perspective on Cancer Drugs Development
Cytel's team of oncology trial design and advanced analytics experts are hosting a series of complimentary webinars...
Read article
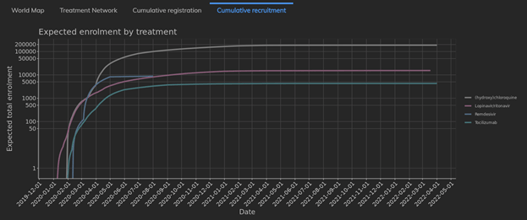
May 1, 2020
Weekly Insights from Cytel's COVID-19 Trial Tracker
There are currently 665 trials registered at Cytel’s COVID-19 Trial Tracker, a jump of over 100 trials in the past two...
Read article
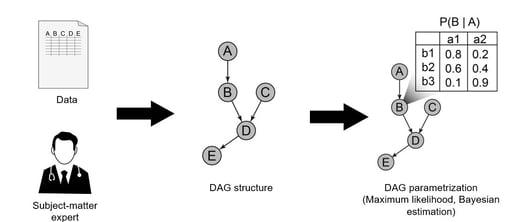
April 29, 2020
Webinar: Transparent Machine Learning in Oncology
In our previous blog, we spoke with Alind Gupta, who works as a Machine Learning Researcher at Cytel in Canada. The...
Read article

April 27, 2020
Highlights from the 2020 Virtual CDISC EU Interchange - Part 2
In the first part of this two-parts blog, I speak about how the European CDISC Committee (E3C) together with CDISC...
Read article

April 24, 2020
Highlights from the 2020 Virtual CDISC EU Interchange by Angelo Tinazzi
In early March, when countries around the world started implementing lockdowns, the European CDISC Committee (E3C)...
Read article

April 23, 2020
A Clinician’s Perspective on Cancer Drugs Development
Cytel is hosting a webinar, “A Clinician’s Perspective on Cancer Drugs Development”, on April 28, 2020. Our speaker,...
Read article
April 23, 2020
Weekly Insights from the COVID-19 Trial Tracker
Every Week Cytel Brings You Further Insights from the COVID-19 Trial Tracker From April 8 through April 17, the number...
Read article

April 20, 2020
Interview with Alind Gupta: Transparent Machine Learning in Oncology
Cytel is hosting a webinar on Transparent Machine Learning in Oncology, on April 21, 2020. Our speaker, Alind Gupta,...
Read article

April 7, 2020
Career Perspectives: Interview with Marc Lefebvre-Gouy, Statistical Programmer
Cytel has industry-leading experts in Statistical Programming with years of SAS® Programming expertise and in-depth...
Read article

April 2, 2020
Remote Working Arrangement – How to get it right?
On March 16, the World Health Organization (WHO) Director-General, Dr. Tedros Adhanom Ghebreyesus, in his media...
Read article
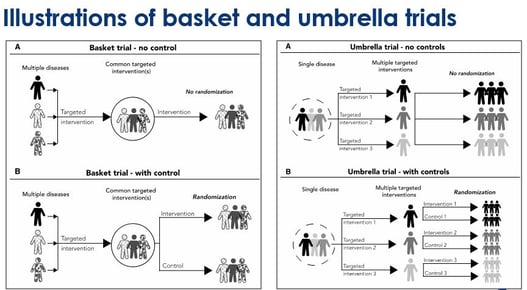
March 31, 2020
Key Design Thoughts for Basket Trials and Umbrella Trials by Jay Park
Since 1953, when the discovery of the structure of DNA was made, we have seen great advancements in genomics....
Read article
March 26, 2020
Cytel's Response: EMA Points to consider on implications of COVID-19
Further regulatory guidance has been released concerning the implications of the Coronavirus disease (COVID-19) on...
Read article

March 23, 2020
Cytel's Response: EMA Guidance on the Management of Clinical Trials During the COVID-19 (Coronavirus) Pandemic
On March 20th the European Commission, the European Medicines Agency (EMA) and the Heads of Medicines Agency (HMA)...
Read article

March 19, 2020
Cytel's Response: FDA Guidance on Conduct of Clinical Trials during the COVID-19 Pandemic
The FDA issued a guidance yesterday on how the COVID-19 Pandemic may affect the conduct of clinical trials. Below are...
Read article

March 12, 2020
Interview with Jay Park: The present and future of Master Protocols
In September 2018, the FDA provided a draft guidance on master protocols reflecting an increased interest in these...
Read article

March 5, 2020
Managing risk in clinical development: Is your data strategy fail-safe?
Generating high-quality clinical data is a vital but challenging task in modern drug development. Unfortunately, in the...
Read article

February 25, 2020
Bayesian Methods for Contending with Homogeneity and Heterogeneity in Real World Data
Over the past decade, a new trend began to emerge, changing the way that clinical trials are conducted. Whereas...
Read article

February 25, 2020
Ensuring an Unbiased Comparator Arm
Regulators in both the United States and Europe have responded positively to the use of SCAs in clinical...
Read article

February 20, 2020
Unlock the power of your clinical data with these five top tips
It is widely acknowledged among drug developers that one of their most important assets is the data generated during...
Read article

February 6, 2020
Is your data strategy set up to tackle key challenges in early clinical development?
In clinical development, a high-quality evidence package is a prerequisite for a new therapy to gain approval from...
Read article
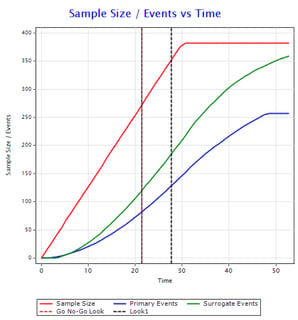
January 30, 2020
Designing Event-based Studies: Interview with Pantelis Vlachos
The Cytel Trial Design Innovations (CTDI) Webinar Series recently hosted a webinar on designing event-based studies....
Read article

January 22, 2020
What could you accomplish with a fresh approach to your clinical data strategy?
In the quest for clinical success, we all strive for evidence packages of the highest quality. If the clinical data is...
Read article

January 16, 2020
Adaptive Population Enrichment in a Phase III Oncology Trial
January’s Cytel Trial Design Innovations (CTDI) Webinar Series will feature Biostatistician and pioneering Bayesian...
Read article

January 8, 2020
How to optimize your data strategy to drive success in clinical development
In clinical development, data is the vital ‘foundation’ that supports your programs. To successfully bring a promising...
Read article

December 18, 2019
Year-End Roundup: Your Favorite Blog Posts of 2019
With only two weeks left for this fabulous year to end, we would like to thank all our blog subscribers and new readers...
Read article

December 16, 2019
Career Perspectives: Interview with Ronald Dumpit, Data Coordinator
Cytel Inc. and Axio Research joined forces in June 2019, expanding our ability to solve the most complex analytical...
Read article

December 10, 2019
Impact of AI on Clinical Development
In association with Statisticians in the Pharmaceutical Industry (PSI) , UCB and Cytel hosted a symposium on September...
Read article

December 5, 2019
Biotechs and Medtechs, don’t forget your market access strategy (part 4 of 4): How to optimize your market access planning approach
Author: Michael S. Paas, Market Access & Commercialization Expert, Executive at AbbVie and Guest Author at Cytel In...
Read article

December 2, 2019
Biotechs and Medtechs, don’t forget your market access strategy (part 3 of 4): Harnessing the value of market access planning
Author: Michael S. Paas, Market Access & Commercialization Expert, Executive at AbbVie and Guest Author at Cytel...
Read article

November 27, 2019
Interview with David Kerr: Data Monitoring Committees (DMCs) – Behind Closed Doors
At the 2019 Challenges in Rare Diseases Clinical Trials Symposium and East training, Cytel partnered with Alexion to...
Read article

November 21, 2019
Biotechs and Medtechs, don’t forget your market access strategy (part 2 of 4): The critical role of market access planning in clinical development
Author: Michael S. Paas, Market Access & Commercialization Expert, Executive at AbbVie and Guest Author at Cytel In my...
Read article

November 14, 2019
Biotechs and Medtechs, don’t forget your market access strategy (part 1of 4): Why is market access strategy crucial to succeed?
Market access strategy is an integral part of the clinical development process to ensure success in global healthcare...
Read article

November 5, 2019
Drug Development in Rare Diseases - Innovation in Statistical Thinking
Cytel is delighted to have Kannan Natarajan speaking at the “Complex Innovative Trial Design Symposium and East User...
Read article

October 23, 2019
The Good Data Submission Doctor - New ADaM Implementation Guidance
October 3, 2019 was an important day for the ADaM team as it marked the release of the ADaM Implementation Guidance...
Read article
October 10, 2019
The Challenges of Rare Diseases in Clinical Trials Symposium and Hands-on East Training
A disease is generally considered to be rare if it affects one patient per 200,000 people (1) and most rare diseases...
Read article

September 12, 2019
Digital transformation in healthcare and drug development
"If you went to bed last night as an industrial company, you're going to wake up today as a software and analytics...
Read article

August 23, 2019
Advancing Medicines Development with External Controls
In place of collecting data from patients recruited for a trial who have been assigned to the control or...
Read article

August 14, 2019
Keeping Clinical Trials on Track: A Statistician's Perspective
This article was originally published as part of a series by pharmaphorum in association with Cytel and is reproduced...
Read article

August 7, 2019
Career Perspectives: Jayshree Garade
In this blog, from our career perspectives series, we talk with Jayshree Garade Associate Director, Statistical...
Read article

August 1, 2019
Predictive Biomarker Signature Characterization
The term biomarker signature describes the behavior of a set of biomarkers that define a signature to maximize the...
Read article

July 22, 2019
Adaptive Design and Health Economic Analysis: Interview with Laura Flight
Health economics and adaptive design methods share common ground in that they both aim to support more efficient and...
Read article

July 8, 2019
Estimands are not just a statistical issue- Q&As and webinar replay
Cytel recently hosted a very well-attended and engaging webinar on the topic of “Estimands, not just a statistical...
Read article

June 27, 2019
Handling the specialized data requirements in oncology clinical trials
By Nicolas Rouillé and Eric Henniger The right design and the right data ultimately leads to the right decisions, so...
Read article

June 14, 2019
Flipping the paradigm-how should biotechs harness adaptive trials?
This article was originally published as part of a series by pharmaphorum in association with Cytel and is reproduced...
Read article




May 7, 2019
Opening the Black Box: Moving to Explainable AI
Nowadays, it’s difficult to pick up a mainstream newspaper or read an industry publication without seeing reference to...
Read article

April 24, 2019
Assuring Outsourcing Obligations with Specialist Data Management Oversight
In this blog, Alla Muchnik, Senior Clinical Data Manager at Cytel, discusses how specialist CROs can add value and...
Read article

April 10, 2019
Ensuring Robust ePRO Implementation: Factors for Success
In this blog, Jonathan Pritchard, Director Business Development at Cytel, draws on his experience in commercial,...
Read article


March 26, 2019
How Patient-Reported Outcomes Improve Outcomes
At the Partnerships in Clinical Trials Conference in Barcelona in November 2018, Strategic Consultant Ursula Garczarek...
Read article

March 20, 2019
Operation Rescue: Addressing Lagging Trials
No one plans to have a trial whose data collection needs rescuing. However, lagging enrollment rates, operational...
Read article

March 15, 2019
Strategic Applications of Pharmacometrics in Clinical Development
Quantitative pharmacology encompasses the many strategic advantages of using complex mathematical models to understand...
Read article


February 28, 2019
Statistical Approaches to Overcome Challenges in Rare Disease Development
In honor of Rare Disease Day 2019 we share a new Cytel podcast featuring Cytel Strategic Consultant Ursula Garczarek...
Read article

February 21, 2019
Podcast with Ursula Garczarek on The Effective Statistician
In 2018, Cytel ran a qualitative survey among biostatisticians and programmers on trends in data science and...
Read article

February 8, 2019
Publication Reveals New Promise for Promising Zone Designs
A 2018 publication in the Biometrical Journal by Cytel’s Cyrus Mehta, Lingyun Liu and Sam Hsiao, ‘Optimal Promising...
Read article

January 30, 2019
Career Perspectives: Interview with Tina Checchio, Associate Director, Quantitative Pharmacology & Pharmacometrics
QPP remains at the heart of model based drug development. Short for Quantitative Pharmacology & Pharmacometrics, it...
Read article

January 10, 2019
Podcast: Overcoming Phase 1 Development Challenges
Nand Kishore Rawat is a Director and Head, Early Phase Biostatistics based in the King of Prussia, PA Cytel office. We...
Read article

December 5, 2018
Creating a Common Language: Forging Statistical and Clinical Collaborations
In this blog, Paul Terrill, Director of Strategic Consulting at Cytel outlines his blueprint for ensuring smooth...
Read article

November 27, 2018
Top 5 Frequently Asked ADaM Questions
This is the third in our blog series ' The Good Data Submission Doctor' in which Angelo Tinazzi, Director of Standards,...
Read article

November 12, 2018
Can Statisticians Contribute to Enhance the Position of Patients in Clinical Trials?
In this blog, we talk with Robert Greene, Founder and President of the HungerNDThirst Foundation, about his upcoming...
Read article

November 8, 2018
Data Management Fundamentals for Your Next Clinical Trial
Data is the most crucial asset in any clinical trial and is used to ultimately drive the decision-making process...
Read article

November 5, 2018
New publication addresses critical issues in ultra-orphan indications
Cytel biostatisticians Cyrus Mehta and Lingyun Liu, together with Charles Theuer, CEO of TRACON Pharmaceuticals have...
Read article

November 1, 2018
Top 5 Frequently Asked SDTM Questions
In this second post of the “Good Data Submission Doctor” ( read my first post The Master Recipe: Quality and Attention...
Read article


October 23, 2018
Career Perspectives: Interview with Munshi Imran Hossain, Senior Data Scientist
Cytel data scientists apply advanced statistical techniques including predictive modeling of biological processes and...
Read article


October 5, 2018
Interview with Stephen Senn: 70 Years and Still Here: The Randomized Clinical Trial and its Critics
We are delighted that Stephen Senn will be joining us at the EUGM on November 14th and 15th in Darmstadt, Germany. In...
Read article

October 1, 2018
Details Matter When Submitting CDISC Packages to Authorities
One of my wife’s favorite TV shows is ‘Quattro Ristoranti’ (Four Restaurants). In each episode of the show, 4...
Read article

September 27, 2018
Decision Making in Development Programs with Targeted Therapies: with Heiko Götte
In this blog, we talk with Heiko Götte, Senior Expert Biostatistician at Merck about his upcoming presentation at...
Read article

September 20, 2018
Career Perspectives: Interview with Adam Hamm, Director of Biostatistics
At Cytel we believe that expert statistical input has the power to shape the future of clinical development: de-risking...
Read article

September 17, 2018
Novel immunotherapies lean on old methods
Immunotherapy has brought us many promises, most notably, of a future where humans are able to harness their body’s own...
Read article

September 10, 2018
Could data science be about to revolutionize the regulatory approval of new drugs?
The biopharmaceutical and healthcare industries now collect more data than ever before due to advances in the variety...
Read article

September 7, 2018
Opportunities of FDA’s Innovative Trial Design Pilot Meeting Program
On August 29th 2018, the FDA announced (1) that it would be establishing a Complex Innovative Trial Design (CID) Pilot...
Read article

September 5, 2018
Podcast: Enhancing Patient Enrollment Forecasting with EnForeSys 2.0
EnForeSys is Cytel’s tool for patient recruitment planning. We have discussed on the blog recently with Tufts...
Read article

August 31, 2018
Highlights from the JSM 2018 Conference
JSM 2018, ASA’s annual gathering of over 6500 attendees attracted statisticians and data scientists to the beautiful...
Read article

August 23, 2018
Career Perspectives: Interview with Meredith Alm, Manager, QA Compliance
Cytel has grown significantly over the last 30 years, with operations across North America, Europe, and India. All of...
Read article

August 21, 2018
How Does a CRO Programming Career Stack Up?
After having spent 15 years in the pharmaceutical industry, in May of 2018, I decided to explore new horizons and took...
Read article

August 15, 2018
2018 East User Group Meeting Addresses Multiplicity Themes, with keynotes including Stephen Senn and Meinhard Keiser.
Cytel’s 7th East User Group Meeting (EUGM) will take place on November 14 & 15, 2018 at Merck in Darmstadt, Germany,...
Read article

August 8, 2018
How can a strategic pharmacometrics consultant add value to your team?
We have written on the blog in the past about the value that a statistical consultant can bring to your team, and to...
Read article
August 1, 2018
Building interactive web applications using R Shiny
By Gordhan Bagri and Munshi Imran Hossain with H A S Shri Kishore Shiny (from RStudio) is one of the most popular R...
Read article
July 27, 2018
Infographic: 5 Key Interactions of Data Management and Statistics
In this blog, we share a new infographic based on this popular blog post illustrating some of the critical interactions...
Read article

July 24, 2018
Career Perspectives: Interview with Sam Hsiao, Associate Director, Strategic Consulting
At Cytel our strategic consulting team works on a wide range of projects including: Identifying the best clinical trial...
Read article

July 18, 2018
Recent Publication: On shapes of ADR report accumulation data
A recent article published by Cytel authors Samadhan Ghubade, Sharayu Paranjpe, Kushagra Gupta, Anil Gore and colleague...
Read article

July 16, 2018
Case Study:Creating an Effective Functional Services Partnership
In this blog we share a case study of how we established and ramped up a functional service outsourcing partnership for...
Read article

July 3, 2018
Unveiling New East 6.5 Modules: Join Our Webinar
It’s shaping up to be a busy year for Cytel’s software development team with a number of upgrades and planned launches...
Read article

July 2, 2018
Highlights from the PSI 2018 Conference
A number of the Cytel team were in Amsterdam, 3rd- 6th June 2018 for the PSI Conference. This year’s conference was...
Read article

June 28, 2018
Non-Compartmental Analysis and the Early Phase Regulatory Environment
By Esha Senchaudhuri With thanks also to Jitendarreddy Seelam and Ramanatha Saralaya for their input. The fact of the...
Read article

June 19, 2018
The Importance of Standardization in Clinical Outsourcing
At the recent PCMG conference in Malta, Adrian Otte ( Independent Consultant, formerly VP Global Development Operations...
Read article

June 14, 2018
What makes a good data manager?
In this blog, Paul Fardy, Executive Director of Data Management at Cytel shares his thoughts on how the data manager...
Read article

May 31, 2018
5 Reasons to Integrate MBMA Into Your Clinical Development Strategy
By Esha Senchaudhuri An important trend in clinical development involves integrating strategic pharmacometric analysis...
Read article

May 23, 2018
Addressing Critical Unmet Oncology Needs in the Era of Precision Medicine
Our Industry Voices series showcases our clients’ innovative work and breakthrough therapeutics in oncologic...
Read article

May 16, 2018
Rewriting the oncology textbook with cell-based immunotherapies
Our Industry Voices series showcases our clients’ innovative work and breakthrough therapeutics in oncologic...
Read article

May 9, 2018
Innovative Oncology Trial Designs in Practice
As we prepare to head to ASCO in under a month's time, we are pleased to share a new ebook that showcases some key...
Read article

April 25, 2018
Overcoming Data Management Challenges in Immuno-Oncology Trials
Data management is an essential building block for successful Immuno-Oncology (I-O) trials. At the Immuno-Oncology...
Read article
April 18, 2018
Developing the Next Generation of Skills for Statistical Programmers
Our recent Clinical Biometrics Survey explored the views of respondents from across the statistical programming,...
Read article

April 13, 2018
Exploring Challenges of Clinical Trial Operations Part 2 with Ken Getz
We return to our discussion with Ken Getz of the Tufts CSDD for part 2 of our blog post on key challenges in clinical...
Read article

April 5, 2018
Ken Getz: Exploring Challenges of Clinical Trial Operations
Photo by J. Kelly Brito on Unsplash Research on clinical trial enrollment makes for sobering reading, characterized by...
Read article

April 3, 2018
Maximizing Preclinical Knowledge for Optimal R&D
By Esha Senchaudhuri In response to its R&D productivity from 2005 – 2010, AstraZeneca took the initiative in 2011 to...
Read article

March 16, 2018
Career Perspectives: Interview with Benjamin Esterni, Principal Biostatistician
At Cytel we believe that expert statistical input has the power to shape the future of clinical development: de-risking...
Read article

March 14, 2018
What makes a Successful FSP Partnership Tick?
Photo by Agê Barros on Unsplash by Natalie Fforde, Senior Director of FSP Services at Cytel With effective use of...
Read article

March 8, 2018
Creating an R-Package Template: A Guide
Photo by Steinar Engeland on Unsplash By Ivan Navarro, Data Scientist at Cytel R is an open-source implementation of...
Read article

March 6, 2018
Best Sample Size Calculators for iPhone
Photo by Dose Media on Unsplash By Charles Liu, Senior Product Manager, Cytel Several years ago, I was one of few...
Read article

February 28, 2018
Insight into the Coordination of Rare Diseases at Sanford registry
There is a consensus in the industry that data on rare diseases is limited, incomplete, and difficult to find or...
Read article

February 27, 2018
Congrats to Lipopharma and CLINGLIO Consortium on Recent Grant Award
We extend our congratulations to Lipopharma and the CLINGLIO project consortium on their recent 6,15M€ grant award by...
Read article

February 21, 2018
Developing efficient tools for ADaM dataset creation
By Diganta Bose, Statistical Programming Team Lead at Cytel Editor's note: This blog is based on work presented at...
Read article

February 15, 2018
A Gatekeeping Procedure to Test a Group Sequential Design
A recent publication in Biometrics ‘A Gatekeeping Procedure to Test a Primary and a Secondary Endpoint in a Group...
Read article

February 13, 2018
Career Perspectives: Interview with Ursula Garczarek, Associate Director - Strategic Consulting
Our strategic consulting team work on projects such as: Identifying the best clinical trial design, implementing...
Read article

February 6, 2018
Life in Programming: Interview With Ajay Sathe
We were excited to learn recently that Ajay Sathe, the CEO of our India Operations, was awarded lifetime honorary...
Read article

January 26, 2018
6 Innovative Trial Design Videos
The Cytel YouTube Channel hosts a wealth of video presentations from Cytel experts as well as external industry and...
Read article

January 23, 2018
Interview: Promoting precision medicine using data science
News Medical interviewed Dr. Rajat Mukherjee, Statistician, and Director of Data Science at Cytel to investigate the...
Read article

January 15, 2018
Addressing the Problem of Feature Selection Using Genetic Algorithms
The problem of feature selection The explosion in the availability of big data has made complex prediction models a...
Read article

January 9, 2018
Career Perspectives: Interview with Lisa Goldberg, Associate Director of Statistical Programming
Our Career Perspectives' series is back! Cytel has industry-leading experts in statistical programming with years of...
Read article

January 3, 2018
How Can We Tackle Heterogeneity in Meta-Analysis?
Health professionals and policy makers want to make healthcare decisions based on the relevant research evidence. The...
Read article


December 12, 2017
Signal Management Using R
Signal management is one of the most audited pharmacovigilance processes. It also generates one of the highest findings...
Read article

November 28, 2017
Interview: Clinical Trial Optimization with R
In this blog we turn to some reading matter, and interview Gautier Paux and Alex Dmitrienko about the recent book...
Read article

November 22, 2017
Career Perspectives: Interview with Makarand Deshmukh, Senior Clinical Data Analyst
Cytel offers a full range of clinical data management services and the team of experts is spread across the globe. In...
Read article

November 15, 2017
Creating Efficiencies in the Vendor Qualification Process: A Proposal
Each year Halloran Consulting Group hosts‘CORE’ (Clinical Operations Retreat for Executives) as a forum for industry...
Read article

November 9, 2017
The Cytel Story: In the Co-Founders' Own Words
In this blog we are excited to unveil a new project which we have been hard at work on over the last few months. 2017...
Read article

November 6, 2017
Asking the Right Questions of Your Data: Experiences in Model Informed Drug Development
At the Chief Medical Officer Summit earlier this year, Cytel's Director of Quantitative Pharmacology and...
Read article

October 31, 2017
Webinar Replay: Dual Target Methods for Go/No-Go Decision Making
As part of Cytel's new Trial Innovations Webinar Series, Pat Mitchell, Statistical Science Director at AstraZeneca...
Read article

October 27, 2017
Design Concept for Confirmatory Basket Trial Interview with Bob Beckman: Part 2
In this blog, we share the second part of our interview with Bob Beckman, about a design concept for a confirmatory...
Read article

October 18, 2017
Webinar Replay: Phase 2 Trial Designs using Program-level Simulations
Cytel's new Trial Innovations Webinar Series provides a platform for the most promising new statistical approaches...
Read article

September 29, 2017
Career Perspectives: Interview with Namrata Deshpande, Senior Team Lead
Namrata Deshpande, Senior Team Lead will be participating in a round table discussion at the Women in Statistics event...
Read article
September 20, 2017
Accurate Event Prediction in a Cardiovascular Outcomes Research Trial
In this blog we share a case study of work our strategic consulting team conducted supporting accurate event prediction...
Read article

September 18, 2017
How to handle conservativeness of Exact p-value?
By Ashwini Joshi For small sample data or rare events data, exact non-parametric tests perform better than asymptotic...
Read article

September 13, 2017
How can Novel Statistical Methods Tackle Antibiotic Resistance?
Antibiotic resistance is one of the greatest challenges facing human health today. We are excited to welcome Dr. Scott...
Read article

September 11, 2017
Design Concept for Basket Trials: Interview with Bob Beckman
At the East User Group meeting (EUGM) on 25th and 26th October, we will welcome a number of renowned industry speakers...
Read article

September 7, 2017
Removing 'Noise' from Biomedical Signals
By Munshi Imran Hossain, Software Affiliate at Cytel Biomedical signals are electrical signals collected from the body....
Read article

August 10, 2017
4 Questions to Explore in Model-Informed Drug Development (Infographic)
Model-informed drug development has been defined by Richard Lalonde ( Lalonde, 2007) (1) as “Development and...
Read article

August 2, 2017
Case Study: Cross-study Efficiencies in Biometrics Outsourcing
As a biometrics -focused CRO, Cytel regularly works across a program of studies, providing data consistency, and...
Read article

July 26, 2017
Are Adaptive Designs the Answer to Oncology Development Success?
Sadly, clinical development of anti-cancer therapeutics faces particularly high rates of failure, even in the context...
Read article

July 19, 2017
Case Study: Seamless Independent Data Monitoring Committee Support
With adaptive and innovative trial designs on the rise, operational implementation of interim analyses, including...
Read article

July 13, 2017
Creating Data Visualizations with R and Shiny
By Tejasweeni Rajput It’s been known for centuries that a picture can tell a thousand words. In an era of new...
Read article

July 11, 2017
Collaboration Brings Success for the UK Adaptive Designs Working Group.
The Adaptive Designs and Multiple Testing Procedures Workshop (ADMTP), the first joint meeting of the Adaptive Designs...
Read article

July 6, 2017
When Biostatisticians Disagree About Ethics
By Esha Senchaudhuri The ethical benefits of adaptive clinical trials have been widely acclaimed: higher prospects for...
Read article
June 28, 2017
Under wraps: the importance of patient privacy
About the Author: Manjusha Gode has over 28 years' IT experience spanning delivery Management, quality management,...
Read article
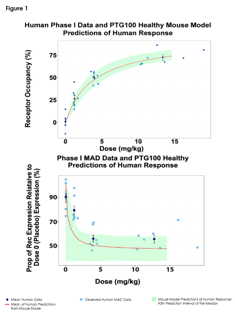
June 12, 2017
Predictions of Pharmacodynamic Responses in Ulcerative Colitis Patient
The Population Approach Group in Europe (PAGE) represents a community with a shared interest in data analysis using the...
Read article
June 8, 2017
Measuring Intergroup Agreement and Disagreement
Cytel's Madhusmita Panda presented at this year’s PSI Conference in the Innovative Methodology session on the topic of...
Read article

May 30, 2017
Interview: How can a Bayesian framework support benefit risk assessment?
A recent paper The case for Bayesian methods in benefit-risk assessment: Overview and future directions (1) co-authored...
Read article

May 26, 2017
Cytel statistical programmer gains recognition at PharmaSUG 2017
PharmaSUG 2017 proved to be an inspirational and informative event. With over 200 paper presentations, posters, and...
Read article

May 22, 2017
Jim Bolognese named 2017 American Statistical Association Fellow
James (Jim) Bolognese, Senior Director, Strategic Consulting, Clinical Services at Cytel Inc. was named a 2017 fellow...
Read article

May 17, 2017
Case Study: From Trial Design to CDISC Submission
This new case study shares how Cytel supported a specialist biopharmaceutical company from Phase 2 trial design through...
Read article

May 4, 2017
The Data Management Perspective on the Interim Analysis
As a recognized expert in adaptive trials, Cytel has extensive experience designing and managing trials with interim...
Read article
April 28, 2017
Case Study: Redesigning a Pragmatic Trial in Oncology
In this blog we share a case study in which our statistical consulting team helped a client redesign an oncology...
Read article

April 25, 2017
Critical Operational Considerations for Interim Analyses
At a recent conference Adam Hamm, Director Biostatistics at Cytel, presented his thoughts on Best Practices and...
Read article

April 11, 2017
FDA 22 Case Studies and Mitigating Phase 3 Risks
In a January 2017 paper (1), the FDA reviewed 22 case studies where promising Phase 2 trials did not result in...
Read article

April 5, 2017
Better Management and Outputs in Statistical Programming
Statistical programmers at all levels can make a significant impact on streamlining delivery, improving efficiency, and...
Read article

March 29, 2017
New Publication: Design and Monitoring of Multi-Arm Multi-Stage Clinical Trials
With an increasing interest in platform designs and other innovative designs that involve multiple comparisons over...
Read article

March 24, 2017
Case Study: Improving Go/No-go Decision-Making with Custom Software
Robust go/no-go (GNG) decision-making is essential for effectively managing risk across a clinical portfolio. In early...
Read article

March 20, 2017
The Role of the Independent Randomization Center
In the randomized clinical trial (RCT), the process of deciding the randomization method and implementing is critically...
Read article

March 15, 2017
The Data Management Plan Takes Center Stage- why is it so important?
A precise and thorough approach to planning is key for success in data management. The Data Management Plan (DMP) is a...
Read article

March 10, 2017
Flexible approaches to Biosimilars Development
At the recent Biosimilars Summit in Philadelphia, Cytel's Pantelis Vlachos presented on statistical challenges and...
Read article

March 2, 2017
Case Study: Bayesian Decision-Making in a Phase 3 Oncology Design
We continue our case study series with this example of a Phase 3 design that uses Bayesian decision making combined...
Read article

February 27, 2017
Estimands 101: Interview with Mouna Akacha
It’s been hard to miss the prevalence of estimand-related discussions in the last year. This is a topic which is very...
Read article

February 21, 2017
Syntax and Variables in R: A Primer
In a previous blog, we provided an overview of basic data structures in R. In this follow up piece, we will provide a...
Read article

February 15, 2017
Outsourcing success for emerging biopharma
Outsourcing solutions should never be a one size fits all process, and smaller and emerging biopharma companies may...
Read article

February 9, 2017
Inside an Oncology Statistician's Toolkit
In this blog, Adam Hamm, PhD, Director Biostatistics at Cytel shares some of the most important knowledge he uses in...
Read article

February 6, 2017
The Making of a CDISC Trainer
CDISC is a global, nonprofit charitable organization whose mission is ‘to inform patient care and safety through higher...
Read article

January 30, 2017
Accelerating development with combined SAD/MAD approach
Single ascending dose (SAD) and multiple ascending dose (MAD) studies are typically the first in human studies. They...
Read article

January 23, 2017
How to get the regulatory green light for your adaptive design?
As a group, Cytel had over 40 successful regulatory interactions last year, many of which supported approvals for...
Read article

January 19, 2017
Data Structures in R: A Primer
R is on the rise in biopharma, and as we have previously discussed on the blog, it is now time for SAS programmers to...
Read article

January 16, 2017
Adaptive Design Approaches from Cardiovascular Clinical Trialists Forum
The Global Cardiovascular Clinical Trialists Forum is a key event bringing together leading experts from across the...
Read article

January 5, 2017
SAS and NONMEM - a marriage made in heaven?
Nonlinear Mixed Effects Modeling (NONMEM) is a type of population pharmacokinetics/pharmacodynamics (popPK/PD) analysis...
Read article

December 21, 2016
CDISC submissions- are you up to speed?
December 18th 2016 was a significant date for the pharmaceutical industry and regulatory submissions. For trials which...
Read article

December 20, 2016
How do CDASH standards build data quality?
Data Standards play a crucial role in structuring and promoting long term value of clinical data. Clinical Data...
Read article

December 15, 2016
Adaptive Design CONSORT Extension Project: The Inside Scoop
In April, we interviewed NIHR research fellow Munya Dimairo about the paper, ‘Adaptive designs undertaken in clinical...
Read article

December 13, 2016
Harnessing the power of R API to extend software applications
In the complex world of trial design and data analysis biostatisticians and data scientists need to ensure they are...
Read article

December 6, 2016
Ensuring quality data no matter the phase: data management considerations
The management of quality clinical data collection is built on a number of core essentials- including project...
Read article
December 2, 2016
Innovative Phase 3 Adaptive Enrichment Design in Oncology
At a recent Pfizer/ Cytel seminar on rare disease and oncology development, Cytel’s Lingyun Liu presented innovative...
Read article

November 21, 2016
Infographic: 10 steps to consider before choosing an adaptive design
While adaptive designs can deliver significant benefits to clinical development- including ethical benefits for...
Read article

November 18, 2016
Case Study: Dose-response modeling informs Phase 2 ulcerative colitis study design
Challenge Our client had the following key questions which they wanted our pharmacometrics group to address for an...
Read article
November 14, 2016
Infographic: 9 Do's and Don'ts to Ensure Independence of QC
In our last blog, we shared some of Angelo Tinazzi and Cedric Marchand's recommendations on how to ensure independence...
Read article

November 11, 2016
How to ensure independence of QC in statistical programming
A solid and robust QC process is one vital component of ensuring quality programming delivery. Angelo Tinazzi and...
Read article

November 9, 2016
New East Insights Video:Creating an SSR Design
Adaptive sample size re-estimation designs are an important part of the statistician's toolkit. In this first in a...
Read article

November 1, 2016
Pharmacometrics tools of the trade: 4 factors to consider
Unlike statistics which has been around in some form for hundreds of years, pharmacometrics is, by comparison, a...
Read article
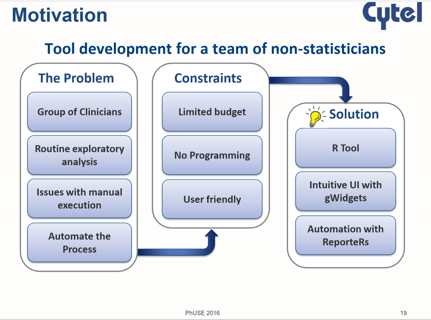
October 25, 2016
R Beyond Statistics
Use of R is a hot topic among statisticians and programmers in the pharmaceutical industry. At the recent PhUSE...
Read article
October 13, 2016
The evolving role of the modern statistical programmer
Statistical programmers play a key role in turning the data from clinical trials into knowledge and supporting the...
Read article

October 11, 2016
Simulations to optimize clinical trial programs
Its important to take a strategic approach to clinical development in order to minimize the potential for Phase 3...
Read article

October 7, 2016
Adaptive Designs: A Data Management Perspective
Adaptive designs have the potential to accelerate clinical development, and improve the probability of trial success....
Read article
October 5, 2016
Challenges in Neuroscience Clinical Trials
While some progress has been made in terms of scientific development in Neuroscience and Neuropsychiatry indications,...
Read article

September 29, 2016
Case studies:Learning from less-well understood adaptive designs
A paper "Best practices case studies for 'less well-understood' Adaptive designs", has been published by the DIA...
Read article

September 27, 2016
Practical Challenges of the LUNG-MAP study
The Lung-MAP trial is an innovative biomarker driven 'precision medicine' study which evaluates five novel agents for...
Read article
September 20, 2016
An efficient tool for model based meta-analysis
Drug development is an expensive and risky business. To maximize a compound’s ultimate chances of commercial as well as...
Read article

September 13, 2016
Case Study:Exposure Response Modeling in Hematology
Exposure-response data gained from clinical studies can provide a basis for model-based analysis and simulation,...
Read article
September 9, 2016
Case Study:Seamless Phase 2/3 Design in Rare Disease
Challenge: Our client, an emerging biotechnology company, was preparing for the next stage of development for their...
Read article

September 7, 2016
Overcoming challenges of 'Less Well Understood' Adaptive Designs
In the 2010 draft FDA ‘Guidance for Industry on Adaptive Design Clinical Trials for Drugs and Biologics', the agency...
Read article

August 31, 2016
An Introduction to BLRM
Traditional rule-based approaches to dose escalation such as 3+3 are widely used in early clinical development. They...
Read article

August 26, 2016
Sample Size Re-Estimation in Bioequivalence Trials with Small Samples
At the recent JSM in Chicago, Cytel’s Sam Hsaio and Lingyun Liu alongside Genentech's Romeo Maciuca, presented a...
Read article

August 23, 2016
How does the T-Statistic stack up for finding MTD?
At the recent JSM meeting in Chicago, Cytel's Jim Bolognese presented the results of work he has conducted evaluating...
Read article

August 17, 2016
Adaptive Designs: In Conversation with the NEJM
Following the recent publication of their review article Adaptive Designs for Clinical Trials in the New England...
Read article
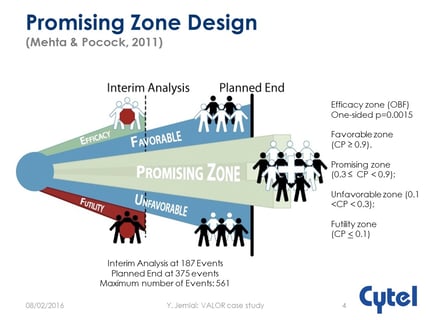
August 9, 2016
Operational and regulatory considerations in a promising zone trial
At the recent JSM Meeting, Cytel’s Yannis Jemiai presented the case study of the VALOR trial which used a promising...
Read article
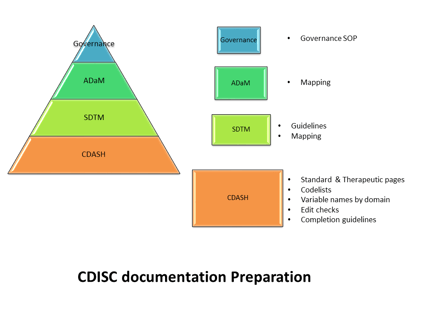
August 2, 2016
The CRO role in Data Standards Governance
Editor's note( this blog was refreshed in April 2018) As CDISC compliant submissions become increasingly expected,...
Read article
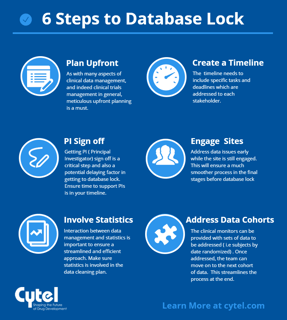
July 28, 2016
6 steps to timely database lock
To close a clinical database right the first time you have to begin with study start-up. Clearly, you can’t close a...
Read article

July 25, 2016
5 trends a statistical programmer needs to follow
Statistical programmers are in high demand within the biopharmaceutical industry, and within the dynamic world of...
Read article

July 21, 2016
Webinar Replay: Single and Double Agent Dose Escalation Designs
Did you miss our webinar on Single and Dual Agent Dose escalation designs earlier in the year? In this blog we have...
Read article

July 18, 2016
Adaptive Design in the limelight with NEJM article
In order for adaptive designs to reach their potential, it’s critical that knowledge is effectively dissemirnated...
Read article

July 12, 2016
Key considerations in selecting an EDC system
How do you go about selecting the best Electronic Data Capture (EDC) system for your study? There is now a vast amount...
Read article

July 7, 2016
Wild Horses: How StatXact is helping conservation project in Mongolia
Why do we do what we do? At Cytel we have always been driven to deliver benefits in the service of human health, and...
Read article
July 5, 2016
PROC MCPMod in Bronchodilator Case Study
At a recent PhUSE SDE, Cytel’s Chitra Tirodkar presented how East PROC MCPMod could be used to help solve the problem...
Read article


June 23, 2016
Getting the best out of your biometrics RFP
Vendor selection is a critical component of ensuring clinical trial success. A 2015 report (1) suggested that clinical...
Read article
June 21, 2016
Sharpening your Advanced SAS Skills: Interview with Sunil Gupta
Sunil is an Associate Director of Statistical Programming at Cytel and has over twenty-five years of experience in the...
Read article

June 16, 2016
Determining the future course of your trial
Predicting the course of a clinical trial is something which people will always want to do-whether for statistical...
Read article
June 14, 2016
Managing DMC analysis- an innovative programming solution
At Cytel, we are very often asked to get involved in DMCs ( Data Monitoring Committees) in a variety of capacities. Our...
Read article

June 7, 2016
How can the CMO/Biostatistician connection improve clinical development?
At the recent CMO Summit East James ( Jim) Bolognese, Cytel’s Senior Director of Strategic Consulting, and Lou...
Read article

May 31, 2016
EAST 6.4 Release: Interview with Yannis Jemiai
Last week, we were delighted to announce the release of East 6.4 bringing further cutting –edge approaches to the East...
Read article

May 19, 2016
Pattern Recognition and 'Big Data'
The explosion in healthcare information and “big data “has been one of the most written about topics in the last few...
Read article

May 17, 2016
Scrambled Data – A Population PK/PD Programming Solution
Cytel participated at PharmaSUG 2016 in Denver recently. A key event on the statistical programming global calendar,...
Read article

May 12, 2016
Lost in Traceability- From SDTM to ADaM
Once upon a time Hansel and Gretel laid a trail of breadcrumbs which they followed to find their way back home. Their...
Read article

May 10, 2016
Subgroup Analyses in Early Phase Clinical Trials
We were fortunate to welcome Björn Bornkamp of Novartis to the EUGM 2016 presenting work he has developed jointly with...
Read article

April 28, 2016
Adaptive Designs in Practice
Adaptive Designs in Practice: Interview with NIHR Research Fellow Munya Dimairo NIHR and University of Sheffield...
Read article

April 26, 2016
Overcoming Data Management Challenges in Oncology Studies
In this blog we’ll highlight some unique challenges that are encountered from a Data Management perspective when...
Read article

April 22, 2016
Dual Agent Dose Escalation Designs
FDA draft guidance on “Co development of two or more unmarketed investigational drugs for use in combination” notes...
Read article

April 20, 2016
Handling CDM data integrations
During the course of any clinical trial, there are often data which, while collected electronically, are outside of the...
Read article

April 15, 2016
5 Key Interactions of Clinical DM and Statistics
It's critical for biostatistics and data management to be closely aligned and working effectively together. The...
Read article

April 13, 2016
HTAs: Adjusting Overall Survival for Treatment Switch
We continue our series of blogs covering the expert presentations from the EAST User Group Meeting. Consultant Claire...
Read article

April 7, 2016
Blinded SSR in early phase biosimilar studies
Francois Beckers, Global Head of Biostatistics & Epidemiology at Merck KGaA joined us at the East User Group Meeting in...
Read article
April 5, 2016
What's the price of pharma innovation?
Cost of pharmaceutical development and R&D productivity is an ongoing industry concern, consistently discussed in the...
Read article

March 29, 2016
Decision Making in Early Clinical Development
On March 16th and 17th the 5th East User Group Meeting took place in London. This very successful 2 days saw a variety...
Read article
March 23, 2016
What's the Value of P?
“How many statisticians does it take to ensure at least a 50% chance of a disagreement about p-values?” So questions...
Read article

March 11, 2016
EAST takes on Multi-Arm Multi-Stage Designs
There has been increasing interest in multi-arm multi-stage trials with treatment selection and sample size...
Read article

March 8, 2016
Mind the Gap! How to prepare for SDTM migrations.
Data standardization is critical to ensure successful regulatory submissions. While many sponsors now choose to create...
Read article
March 3, 2016
Adaptive SSR: Debunking the inefficiency myth
'The aim of a discussion should not be victory but progress.' This principle, expressed by the French essayist Joseph...
Read article

February 26, 2016
Getting Technical: The evolving role of the Data Manager
Remember the early days of Electronic Data Capture? Those first systems, which were revolutionary for their time...
Read article
December 3, 2015
"Data Standards and My Experience" - Reflections from Sangeetha Gandepalli
On Dec. 12, 2015 Sangeetha Gandepalli, a Technical Lead in Clinical Data Management at Cytel, will speak before SCDM...
Read article
December 1, 2015
Making the Most of Data Management for Risk Based Monitoring
Risk based monitoring is a strategic monitoring practice which aims to shine the spotlight on problematic study areas,...
Read article
November 12, 2015
2 Talks on Early Phase Go/No-GO Decision Making
Last week Cytel joined forces with Sanofi/Genzyme to devote a full day of workshops and talks related to modern methods...
Read article
November 10, 2015
Bayesian Dose Escalation Designs for Late Onset Toxicity
Last week Cytel joined forces with Sanofi/Genzyme to devote a full day of workshops and talks related to modern methods...
Read article
November 5, 2015
The 24 Hour Work Day
Oftentimes people perceive a tradeoff between speed and quality. The faster you do something the more likely you are to...
Read article
November 3, 2015
Pharmacometrics for Biomarker Driven Clinical Strategy
QPP (sometimes called QP2) remains at the heart of model based drug development. Short for Quantitative Pharmacology &...
Read article
October 29, 2015
How to Reduce Bias in the Estimates of Count Data Regression
A common challenge of working with small sample sizes is determining proper bias correction methods when evaluating a...
Read article
October 27, 2015
P-Values & Pharma Development: We Want to Hear from You
Here at Cytel we have enjoyed following the debates on the p-value controversy currently taking place on the ASA...
Read article

October 19, 2015
3 Statistical Challenges for Pooling Phase 1 Data
It is often necessary to pool safety data from late phase studies, in preparation for regulatory submission. Some of...
Read article
October 15, 2015
MCPMod: An Introduction
The method for dose-response modeling that is widely called MCPMod allows a sponsor to measure the likelihood that...
Read article
October 13, 2015
Statistical Primer for Cardiovascular Research
In honor of World Obesity Day (celebrated on Oct. 11 2015) here is an American Heart Association Statistical Primer on...
Read article
October 8, 2015
Being a Statistician: An Art, a Science or Just Job?
A recent American Statistical Association conference featured a town hall meeting to discuss the role of the...
Read article
October 5, 2015
2 Methods for Evaluating Biomarker Subpopulations | Cytel
One consideration every sponsor of a biomarker-stratified confirmatory trial must take into account, is whether to...
Read article
October 1, 2015
It’s Time to Bridge the Gap Between Pharmacometrics and Biostats
This week marks the sixth annual American Conference on Pharmacometrics, held this year in Crystal City, VA. Situated...
Read article

September 29, 2015
5 Skills Needed by All Highly Effective Statisticians
The Head of the DIA’s Adaptive Design Working Group Asks Us to Consider 5 ‘Soft-Skills’ All Effective Statisticians...
Read article
September 24, 2015
Virtual Teams and Clinical Data Management
Earlier this week, Patti Arsenault, Cytel’s Global Head of Clinical Data Management, sat on an SCDM panel with members...
Read article
September 17, 2015
Inference on Confidence Intervals for Adaptive Designs: The Latest Breed of Adaptive Clinical Trials
Most people familiar with adaptive clinical trial designs are familiar with those statistical designs that reject the...
Read article


September 4, 2015
Using Simulation for Accelerated Early Phase Drug Development
Our Client's Challenge: Can knowledge of the relationship between biomarkers and clinical endpoints help us to optimize...
Read article
September 1, 2015
Modern Early Phase Clinical Trial Design Primer
If you’re in the practice of conducting early phase clinical trials, you’ve probably heard that modern trial designs...
Read article

August 13, 2015
Do you really need a full service CRO? An exploration of strategic options
Full service or specialized? Full service or specialized? For many looking to hire a CRO, the answer is obvious....
Read article
August 10, 2015
Mitigate Phase 3 Clinical Trial Risk by Optimizing Phase 2 Data
When approaching a Phase 3 clinical trial, the need to ‘de-risk’ the massive investment often leads sponsors on a quest...
Read article
July 27, 2015
Evidence Based Medicine: 25 Years Later
We were saddened to learn earlier this year, of the passing of Professor David Sackett. Widely recognized as the father...
Read article

July 21, 2015
MCP-Mod for the Modern Dose-Ranging Clinical Trial
MCP-Mod methodology for dose-ranging clinical trials has been gaining popularity since the 2013 publication of the...
Read article

July 14, 2015
Why and When to Use Profile Likelihood Based Confidence Intervals
When conducting Maximum Likelihood Estimation, it is assumed that the maximum likelihood estimate follows a normal...
Read article
June 26, 2015
Clinical Trials: Why You Should Not Power for Superiority Upfront
Powering a trial for superiority can be financially risky. In some instances it may also prove unnecessary.
Read article

June 25, 2015
3 Strategies to Combat Inferential Conservatism in Small Sample Sizes
When conducting a clinical trial with small or sparse data sets, statistical methods meant for large sample sizes may...
Read article
June 18, 2015
A Cautionary Tale about Composite Endpoint Construction: The ARISE Trial
In August 2006 AstraZeneca completed the ARISE trial, which aimed to determine whether AGI-1067 was effective in...
Read article
June 11, 2015
Aligning Clinical Development & Regulatory Objectives for Cardiovascular Outcome Trials
When the FDA first began to require pharmaceuticals to perform cardiovascular outcome trials to establish the safety of...
Read article
June 5, 2015
Building Teams to Handle Unexpected Regulatory Agency Requests
Not long ago, one of our clients submitted Phase 2 and Phase 3 data for a new rare disease drug which had received...
Read article
June 4, 2015
Patient Recruitment Feasibility: Would you bet $12 million dollars on it?
Two insightful papers from Applied Clinical Trials should be of interest to many clinical trial planners. The first by...
Read article

May 28, 2015
How to Use Outsourcing to Reduce Clinical Development Risk
Risks in drug development range from taking the wrong drugs forward to Phase 3 to investing in a drug development...
Read article

May 20, 2015
Seamless Adaptive Clinical Trials: What’s really at stake?
Seamless adaptive clinical trials have gained popularity for reducing the projected time it takes to complete the...
Read article

May 15, 2015
Can You Reproduce Your Clinical Trial Results?
Imagine that it’s been three years since the completion of a trial, and that suddenly a regulatory body calls into...
Read article

May 14, 2015
Marvin Zelen's 8 Predictions for the Future of Biostatistical Sciences
Ten years ago, in May 2005, world-renowned biostatistician Marvin Zelen was asked to deliver a keynote address before...
Read article

April 30, 2015
New Articles on Adaptive Clinical Trials & Adaptive Financing
Adaptive financing (not to be confused with adaptive licensing) explores how biotechs, pharmaceuticals and potential...
Read article
April 23, 2015
Dose-finding with Sequential Parallel Comparison Designs
Last week the Cytel Blog discussed the benefits of using the Adaptive Maximizing Design [AM Design] for dose-finding...
Read article
April 21, 2015
Adaptive SSR for Small Sample Sizes?
“We shouldn’t use an adaptive design, our sample size is too small.” Most clinical trial planners have heard this line...
Read article
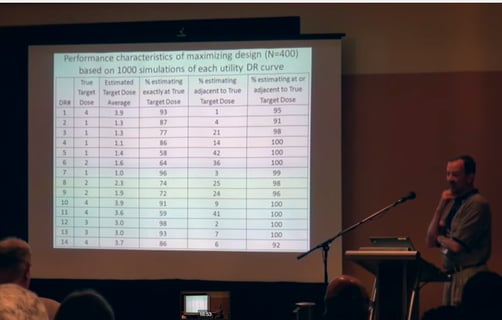
April 16, 2015
Phase 2 Designs for Clinical Utility Limiting Therapies
When testing certain types of new drugs it is known in advance that the adverse side-effects of the medication will...
Read article

April 13, 2015
New Cytel Whitepaper: Monte Carlo Simulations for Patient Recruitment
Cytel has published a new whitepaper on Monte Carlo Simulations for Patient Recruitment, which illustrates how a...
Read article
April 9, 2015
Relative Clinical Efficiency and Phase 2 Biomarker Studies
Last year. Nature Reviews Drug Discovery asked the FDA’s Tatiana Prowell (Hematology & Oncology Products Division)...
Read article
April 2, 2015
Monte Carlo Simulations II: Reassessing Strategic Options During an Interim Look
Midway through a trial is a terrible time to realize that you need a new strategy to complete the study. Sadly, it is...
Read article
March 27, 2015
Leveraging the Flexibility of an Adaptive Clinical Trials: A Case Study
We have often said that one of the greatest benefits of an adaptive clinical trial is the flexibility it affords for...
Read article
March 26, 2015
Statistical and Operational Challenges of the VALOR Trial
Last year Sunesis completed the VALOR trial, the first clinical study to make use of the groundbreaking promising zone...
Read article
March 20, 2015
How Bayesian Strategies Can Expedite a Pediatric Clincial Trial Time by 20 - 40%
Sometimes a new candidate drug for a pediatric study has already been tested on adults for safety and efficacy. We know...
Read article
March 19, 2015
How to Plan Interim Looks in Adaptive Clinical Trials: 3 Strategies
A well-timed interim analysis can generally supply added benefits to the operational and administrative aspects of a...
Read article
March 12, 2015
Monte Carlo Simulations for Patient Enrollment: A Presentation
Recently, we published an interview with Chris Conklin, the Director of the Center for Feasibility Excellence at...
Read article
March 10, 2015
Embracing the Adaptive Mindset
Most of us are primed to think about the design of adaptive clinical trials as a narrow set of techniques applied to a...
Read article
March 5, 2015
Adaptive vs. Group Sequential Designs in Survival Analysis
The Mehta-Pocock promising zone is often used to carry out unblinded sample size re-estimation during interim analysis....
Read article
February 26, 2015
Successful Adaptive Confirmatory Dose-Response Pediatric Study
Cytel President and co-founder Cyrus Mehta has co-authored a paper on Infantile Hemangioma, recently published in the...
Read article
February 17, 2015
How Proposed Regulatory Reforms Will Affect Your Clinical Trial
21st Century Cures (also called Cures2015) is a bipartisan initiative undertaken by the Committee on Energy and...
Read article
February 12, 2015
Data-Driven Trial Planning: An Interview with Pfizer's Chris Conklin
Data driven decision-making can ensure that every feasibility team achieves its enrollment milestones. By transforming...
Read article
February 10, 2015
How to Shorten a Cardiovascular Outcome Trial By Two Years
Cardiovascular outcome trials (CVOTs) have earned the reputation of being the untamable behemoths of the clinical...
Read article
February 5, 2015
3 Key Trends in Clinical Trial Enrollment Forecasting
Every clinical trial requires some manner of trial forecasting, normally for feasibility and patient enrollment....
Read article
February 3, 2015
Clinical Development & Statistical Methodology for Cardiovascular Risk Assessment
A new publication co-authored by Cytel Co-Founder and President Cyrus Mehta considers a range of clinical development...
Read article
January 29, 2015
Adaptive Design and Bayesian Statistics: 5 Years Later (Podcast)
February 2015 marks the five year anniversary of the FDA’s Guidance on Adaptive Design Clinical Trials for Drug and...
Read article
January 27, 2015
How to Take Control of Your Enrollment Woes
Last week we released an infographic on why Phase 3 trials fail. The numbers, while eye-opening, did not capture a...
Read article
January 22, 2015
Adaptive Clinical Trial Strategies for the Limited Early Phase Budget
The Journal of the American Medical Association recently published an article entitled ‘The Anatomy of Medical...
Read article
January 20, 2015
Why Drugs Fail in Phase 3: A Cytel Infographic
According to a recent Cytel Whitepaper on Adaptive Clinical Trials, 50% of Phase 3 trials eventually fail. This new...
Read article
January 16, 2015
Old and New Drug Development Paradigms: Cytel Infographic
Adaptive designs are thought to be the new paradigm in drug development, allowing statisticians and trial designers to...
Read article
January 13, 2015
Simulation and Prediction for Adaptive Licensing Decision-Making
Janus was the Roman God of transitions, a deity with two faces, one looking towards the past and the other the future....
Read article
December 18, 2014
Early Phase Development Strategy: Bayesian Methods for Go/No-Go Rules
Earlier this week, we at Cytel enjoyed a riveting in-house discussion on the uses of Bayesian decision rules for...
Read article
December 16, 2014
Cultivating Versatility in Statistical Consultants
Richard Branson once wrote: “I have always valued capability over expertise. While you may need to hire specialists for...
Read article
December 11, 2014
Adaptive Designs for Infectious Diseases Clinical Development Strategy
A common framework for the clinical development of vaccines involves the study of several candidate compounds in Phase...
Read article
December 9, 2014
Drug Supply Planning for Dose-Ranging Adaptive Trials
When planning a conventional trial, one can anticipate the drug supply necessary for the trial by determining how the...
Read article

December 4, 2014
Operationally Seamless & Inferentially Seamless Adaptive Designs
Fulyzaq® from Napo/Salix was the first drug ever to be approved using an adaptive two-stage "seamless" clinical trial...
Read article
December 2, 2014
How to Incorporate New Technology into Your Clinical Development Strategy
During a recent DIA webinar on reinventing the clinical trial, Laurie Halloran (President of the Halloran Consulting...
Read article
November 18, 2014
A Bayesian Industry Approach to Phase I Combination Trials in Oncology
Statisticians and scientists at Novartis have been at the forefront of developing a new method in early phase oncology...
Read article
November 17, 2014
Remembering Marvin Zelen
Outstanding Thought Leader, Scientist and Humanitarian, Passes away at Age 87 It is with immense sadness that we...
Read article
November 12, 2014
Ranking Adaptive Dose-Finding Designs using Clinical Utility Functions
Clinical utility functions provide Phase 2 trial sponsors with an intuitive metric by which to measure the quality of a...
Read article
November 6, 2014
Translational Statistics: How to Move Beyond the Comfort Zone
Professor LJ Wei holds that rules are for lawyers, not (necessarily) clinicians. When designing modern clinical trials,...
Read article
November 4, 2014
New Exploratory Trial Method Translates into Better Financial Strategy
A key stage of exploratory drug development is implementing a proof-of-concept study to demonstrate the safety of a...
Read article
October 30, 2014
Michael Proschan on Blinded Adaptations, Permutations and t-tests
During last week’s East Users Group Meeting, Michael Proschan of the NIH and NIAID, gave a presentation on ‘Blinded...
Read article
October 28, 2014
Adaptive Dose Finding Using Toxicity Probability Intervals
Phase 1 oncology trials typically use either rule-based methods or model-based methods to determine the most acceptable...
Read article

October 21, 2014
Clinical Impact Beyond 'Time to First' Analyses
Every year, the East Users Group Meeting brings together notable experts from industry and academia to discuss the...
Read article
October 14, 2014
7 Reasons to Add a Statistical Consultant to Your Team
We are often asked how statistical consultants can add value to the clinical development process. What do they...
Read article
October 7, 2014
You Own This!
Guest blogger Laurie Halloran is the President and CEO of Halloran Consulting Group, a management consulting firm for...
Read article
October 2, 2014
Bayesian-Bandit Adaptive Designs for Rare Disease Drug Development
Sofia S. Villar is a member of the DART (Design and Analysis of Randomised Trials) group at the MRC Biostatistics Unit...
Read article
September 25, 2014
Part II: The Philosophy Behind a Software Package
A few weeks ago, we posted a synopsis of an event held at ISCB Vienna in which statisticians from Cytel, SAS and Stata...
Read article
September 23, 2014
Adaptive Clinical Trials: Your Questions Answered
If you're a company considering an adaptive trial for the first time, you probably have many questions. One of our...
Read article
September 18, 2014
5 times ‘Keep it Simple’ May Be Bad Advice for Clinical Designers
When designing clinical trials, many trial designers are advised to keep the trial simple. Prima facie, the keep it...
Read article
September 11, 2014
Empirical Study Confirms Positive Impact of Adaptive Designs
According to a recent Impact Report from the Tufts Center for the Study of Drug Development, 21% of active clinical...
Read article
September 4, 2014
Adaptive Designs for Evidence Based Oncology: Insights from the Experts
Imagine if we were to count the number of possible reasons that investigators might have for monitoring a biomarker...
Read article
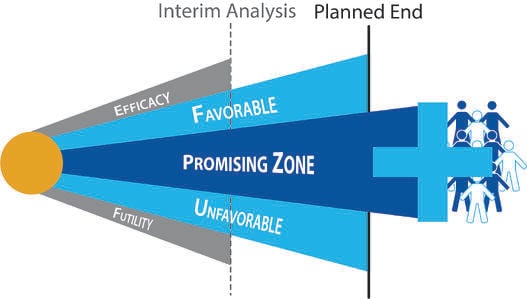
September 2, 2014
Impact of Study Design and Development Strategy on Pharmaceutical Programs and Portfolios
As more clinical trials make use of adaptive designs, investors have come to realize that high quality trial designs...
Read article

August 26, 2014
Statisticians from Cytel, SAS and Stata talk Software Development
During an invited speakers session at the lnternational Society for Clinical Biostatistics, Cytel VP Yannis Jemiai was...
Read article
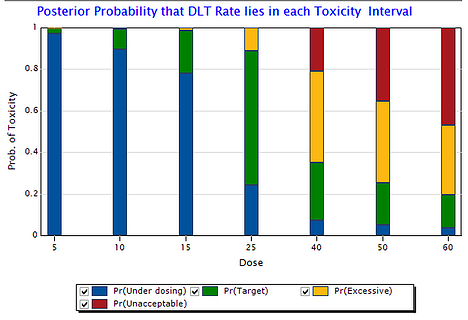
August 21, 2014
Bayesian Trial Designs are Safe, Efficient & Flexible: A Review of Published Phase 1 Studies
Use of the continual reassessment method (CRM) is safe, efficient, and flexible, according to a comprehensive review of...
Read article
August 14, 2014
Backward Image Confidence Intervals for Adaptive Group Sequential Designs (Full Article Attached)
Cytel statisticians are looking foward to attending the Conference of the International Society for Clinical...
Read article

August 12, 2014
What Horsepower Can Teach us about Well-Powered Trials
Beyond Wild Horses: Developing Innovation at Cytel "Horse-and-pony" by arjecahn on flickr. -...
Read article
August 5, 2014
Reflections on Statistical Entrepreneurship: An Interview with Nitin Patel
Cytel CTO Nitin Patel, recently sat down with ECHOES (a magazine for statistics in clinical trials) to discuss his...
Read article
July 31, 2014
Bayesian Approaches in Clinical Trials: Updates on Tools & Techniques
Statisticians at Cytel are staunch advocates of the use of Bayesian methods in clinical trials. This summer's Joint...
Read article

July 29, 2014
Why Using Adaptive Designs Can Attract Investors to Your Trial
Adaptive designs are the unsurprising hot topic of this year’s Joint Statistical Meeting, which features over one...
Read article

July 24, 2014
Data Management and Biostatistics III: Statistical Innovation in Clinical Data Management
This is the third post in a three part series in which we consider (i) improvements to trial quality that result from...
Read article

July 22, 2014
10 Simple Steps to Deciding Whether Your Next Trial Should be Adaptive
PROCYSBI, the first drug to receive FDA approval after following an adaptive population re-assessment design, was one...
Read article
July 17, 2014
Predicted Interval Plots: A General Overview
In anticipation of Cyrus Mehta’s webinar next week on new predictive analytics tools for trial forecasting, we thought...
Read article

July 15, 2014
Cytel Animation: Modern Dose Escalation Phase 1 Trials
Do you design or analyze Phase 1 dose escalation trials? Have you considered methods other than 3+3? This new Cytel...
Read article
July 10, 2014
Designs for Biomarker Driven Population Enrichment in Oncology
Complexities with identifying suitable test populations in oncology studies contribute significantly to the 60%...
Read article
July 8, 2014
5 Reasons to Invest in Adaptive Designs for Population Enrichment
The above graphic is from Cyrus Mehta's slides on 'Adaptive Population Enrichment for Oncology Trials with Time to...
Read article
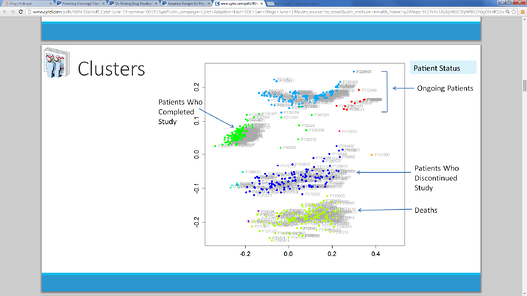
July 1, 2014
'Multivariate Approaches for Risk-Based Monitoring' An Adaptive Design (Slides Attached)
A recent Cytel Seminar on Adaptive Statistical Designs featured a talk by Michael Elashoff (Patient Profiles) on...
Read article
June 26, 2014
Adaptive Designs for Precision Medicine: A Look at Pfizer
The rise of biomarker based treatments in oncology has meant a reconceptualization of what constitutes a particular...
Read article
June 10, 2014
Cytel Weighs in on Strategies for Oncology Development
The FDA’s Tatiana Prowell (Breast Cancer Scientific Lead in the Office of Hematology & Oncology Products) recently gave...
Read article
June 5, 2014
Powering Oncology Trials for Success: Adaptive Designs in East
Charles Liu, PhD, Cytel Statistician and Product Manager In the US, cancer is the most common cause of death after...
Read article

June 3, 2014
Data Management & Biostatistics II: Operational Benefits of Bundling
This is the second post in a three part series in which we consider (i) improvements to trial quality that result from...
Read article
May 29, 2014
2014 Zelen Award Honors Statistician and Educator
Cytel has taken the initiative to train the next generation of clinical programmers through its innovative Clinnical...
Read article

May 22, 2014
Data Management & Biostatistics I: Improving Trial Quality
This is the first of a three part post in which we will consider (i) improvements to trial quality that result from...
Read article

May 19, 2014
Frequentist? Time for an update!
Pantelis Vlachos, PhD, is a Director at Cytel Consulting. He works with a team of experts who regularly assist clinical...
Read article

May 13, 2014
De-Risking Drug Development using Adaptive Design
The VALOR trial recently applied a promising zone design to a Phase 3 evaluation of Vosaroxin, a candidate for the...
Read article
May 8, 2014
5 Reasons to Invest in Bayesian Dose-Escalation Methods
( Editor's note: This post has been refreshed in December 2016) Model based algorithms for Phase I dose-escalation have...
Read article
May 5, 2014
The Perils of Poor Recruitment
A new JAMA study on discontinued randomized trials in Switzerland, Germany and Canada, reports that poor recruitment...
Read article

April 30, 2014
StatXact 25th Anniversary: Reflections of a Pioneer
For the second installment of our StatXact 25th Anniversary Retrospective Series, Professor Joan Hilton (UC San...
Read article
April 24, 2014
New JAMA Study Confirms Importance of Trial Design for FDA Approval
Here at Cytel we firmly believe that if you don’t get the design of a clinical program right, then nothing else...
Read article

April 21, 2014
StatXact 25th Anniversary: A Horizon for the Stars
The core methodological problem that would eventually spur the development of Cytel’s StatXact software was first posed...
Read article


