When conducting Maximum Likelihood Estimation, it is assumed that the maximum likelihood estimate follows a normal distribution. However, this may not be true in the case of small sample or sparse data.
Since the standard errors of the general linear model are based on asymptotic variance, they may not be a good estimator of standard error for small samples. In particular, Wald Confidence Intervals may not perform very well. One should only use the Wald Confidence Interval if the likelihood function is symmetric about the MLE.
In cases where the likelihood function is not symmetric about the MLE, the Profile Likelihood Based Confidence Interval serves better. This is because the Profile Likelihood Based Confidence Interval is based on the asymptotic chi-square distribution of the log likelihood ratio test statistic.
More specifically, when using the Wald Confidence Interval, two points on either side of MLE are chosen such that they are equidistant from MLE value (MLE ± SE * (1-alpha)/2 percentile of Normal distribution). However, when using the Profile Likelihood Based Confidence Interval, two points on either side of MLE are chosen such that likelihood at those two points is equal to (maximum likelihood – ½ * (1-alpha) percentile of the chi-square distribution with DF 1).
Case Study Using LogXact 11
Please refer to the diagrams below for graphical understanding.
Data: Animal.cyd (Please note that this is binary data but we can apply Poisson regression as there are only 4 events in 72 cases)
Penalized Poisson regression for stratified data
Stratum: strata
Model: Aneur ~ NoHep
Here SE of MLE is large (6.118e+005) indicating non-convergence.
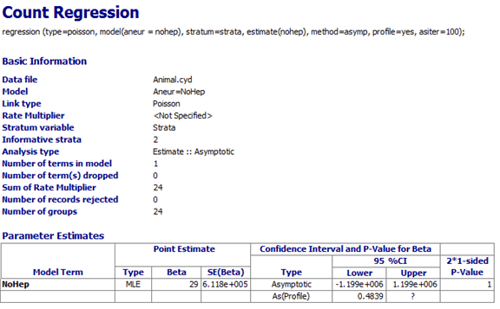
However, selecting Penalized Likelihood gives the following result:
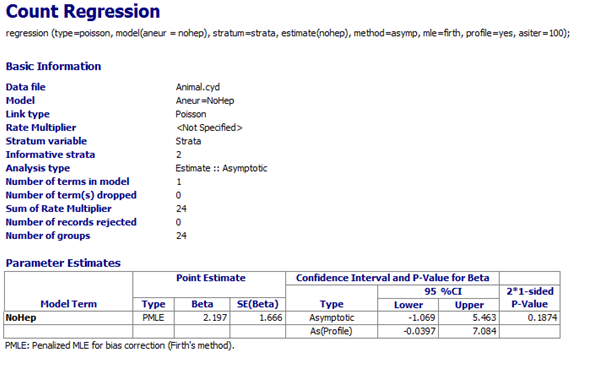
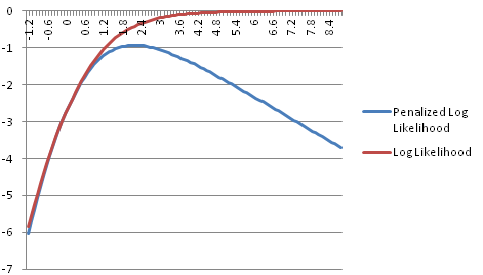
Here PMLE gives reasonable output when MLE had large standard error as shown in the following graph:
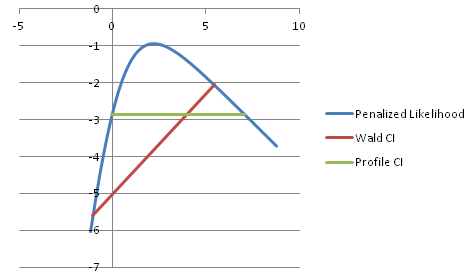
In the following graph, we can see how Profile likelihood based Confidence Intervals are better than Wald Confidence Intervals in the case of an asymmetric likelihood function.
Liked this article? Click the button below to download a copy to read off line.
Interested in a 30 day trial of LogXact? Click the button below to request.
Related Items of Interest
[1] LogXact 10 Manual.[2] Heinze G., Ploner M. (2004), A SAS macro, S-PLUS library, and R package to perform logistic regression without convergence problem.
[3] Venzon D.J., Moolgavkar S.H. (1988) , A method for computing Profile-Likelihood- Based intervals, Applied Statistics, 37;1:87:94.
